1. Устойчивость в широком смысле. Примеры устойчивости и неустойчивости. Определение устойчивости по Л.М. Ляпунову. Асимптотическая устойчивость.

2. Устойчивость линеаризованных АС. Условие асимптотической устойчивости линеаризованных АС. Теоремы Ляпунова об устойчивости линеаризованных АС.

3. Алгебраический критерий устойчивости Гурвица. Частные случаи.

4. Частотный критерий устойчивости Михайлова. Следствие из него (критерий чередуемости корней).

5. Частотный критерий устойчивости Найквиста в случае устойчивой разомкнутой АС.

6. Частотный критерий устойчивости Найквиста при наличии в структуре разомкнутой АС интегрирующих звеньев.

7. Частотный критерий устойчивости Найквиста в случае неустойчивой замкнутой АС. Обобщенный критерий устойчивости Цыпкина.

8. Логарифмический критерий устойчивости Найквиста. Обобщенный логарифмический критерий устойчивости.

9. Понятие о запасах устойчивости. Общепринятые запасы устойчивости (запас по фазе и амплитуде).

10. . Области устойчивости. Построение областей устойчивости с использованием известных критериев устойчивости.

11. Качество АС. Перечислить показатели качества переходного процесса АС, дать каждому из них определение.

12. Понятие о прямых оценках качества переходного процесса. Косвенные оценки качества. Корневые оценки качества переходного процесса.

13. Частотные оценки качества переходного процесса (по АЧХ и вещественной частотной характеристике замкнутой АС).

14. Интегральные оценки качества переходного процесса.

15. Точность АС. Вычисление ошибок по отношению к задающему воздействию. Структурный признак астатизма по отношению к задающему воздействию.

16. Вычисление ошибок по отношению к возмущающему воздействию. Структурный признак астатизма по отношению к возмущающему воздействию.

17. Понятие о синтезе и коррекции АС. Построение желаемой ЛАХ.

18. Синтез последовательного и параллельного корректирующих устройств.

19. . Нелинейные АС. Типовые нелинейности в автоматике.

20. Особенности динамики нелинейных АС. Автоколебания, механизмы их возникновения и анализ с применением энергетических диаграмм.

21. Фазовое пространство и его смысл для анализа нелинейных АС. Фазовая плоскость. Свойства фазовых траекторий.

22. Особые точки фазовой плоскости. Типы простых особых точек и их фазовые портреты (по таблице).

23. Особые кривые и области фазовой плоскости, их фазовые портреты.

Кроме перечисленных вопросов необходимо владеть минимумом остаточных знаний из

первой части курса в виде определений и понятий: автоматическая система (АС); объект управления; регулятор, обратная связь; принцип управления по отклонению; астатическая и статическая АС; передаточная функция; переходная функция; комплексная передаточная функция; АЧХ; ФЧХ; логарифмические частотные характеристики; формулы типовых соединений звеньев; передаточные функции замкнутых АС; построение ЛАХ разомкнутых АС.

1. Устойчивость в широком смысле. Примеры устойчивости и неустойчивости. Определение устойчивости по л.М. Ляпунову. Асимптотическая устойчивость.

Устойчивость системы- способность системы сохранять свои свойства достаточно длительный промежуток времени, при действии на нее возмущающих факторов.

Это критерий физической реализуемости свойств системы а следовательно и самой системы.

Неустойчивость системы также важна

Только при неустойчивости можно получить устойчивую систему.

Важнейшим свойством действительности является движение в том числе относительный покой.

Движение АС- изменение ее выходной координаты y(t)

Невозмущенное движение-движение, для реализации которого создано АС при заданном выходном сигнале.

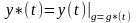-невозмущенное(1)

Всегда существуют малые причины отклонения в силу которых могут возникать большие следствия.

При устойчивости малые причины не должны вызывать больших отклонений от невозмущенного движения.

Теория устойчивости Ляпунова.

Возмущение- отклонение Н.У. от нулевых.

Любое движение, отличное от невозмущенного назовем возмущенным

-отклонение возмущенного движения от невозмущенного.

• y(0)-начальное отклонение возмущенного движения от невозмущенного

ОпределениеЕсли для сколь угодно малого положительного произвольного числа найдется такое положительное число такое что из условия следует что при t>0 то невозмущенное движение будем считать устойчивым.

Если с течением времени возмущенное движение сколь угодно близко приближено к невозмущенному, то невозмущенное движение называется асимптотически устойчивым

2Е-полоса возмущающего дв-я

Невозмущающ. устойчивое движение y(t)- если для любых НУ в полосе 2кпд

Возмущ. Дв-е не выходит из полосы 2

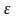
2-я неустойчивая кривая,т.к касается границы.

2. Устойчивость линеаризованных ас. Условие асимптотической устойчивости линеаризованных ас. Теоремы Ляпунова об устойчивости линеаризованных ас.

Пусть имеется АС вида:

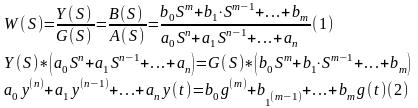
Подадим на вход АС. Сигнал 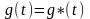для получения на выходе желаемого сигнала и применим это движение за невозмущенное

(3)

Получит 3 можно доставить g(t) в правую часть уравнения (2)

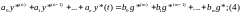
Пусть начальные условия невозмущены ( не нулевые)

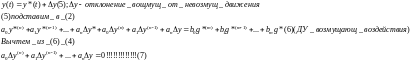
Тоесть, если в ДУ(1) ввести возмущение, то также получаем 0

Вывод: в линеаризованных АС устойчивость не зависит от внешних воздействий. В нелинейных системах это не так. Линейных систем не существует.

Нелинейность:

Условие ассимптотиечкой устойчивости.

Очевидно, что для ассимтотиечской устойчивости необходимо, чтобы

-отклонение возмущенного движения от невозмущенного.

Из ДУ возмущенного движения определим условия при которых это возможно

Для решения необходиомо записать характеристическое уравнение

Рассмотрим 2 случая. Будем считать корни характеристического уравнения различными. Другие случаи на практике.

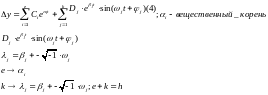
чтобы из 4 получить условие необходимо чтобы показатель экспоненты был отрицательным.

Для устойчивой замкнутой АС необходимо и достаточно чтобы вещественные части корней характеристического уравнения замкнутой АС были строго отрицательными.

Остались 2 проблемы:

1. Все реальные системы нелинейны. И возникает вопрос « при каких условиях устойчивость линеаризованной АС влечет устойчивость исходной нелинейной

2. Методика построения характеристического уравнения замкнутой АС.

1-я проблема решается с применением Теоремы Ляпунова

Смысл теорем Ляпунова в том, что они дают критерий, когда устойчивость линейной влечет устойчивость исходной нелинейной.

Теорема 1(об устойчиовсти): Если линеаризованная система ассимптотически устойчива, то исходная нелинейная также устойчива., если возмущенные Н.У. сколь угодны малы.

Теорема 2( о неусточивости): Если линеаризованная система неутсойчива, то исходная нелинеейная также неустойчива

Теорема 3( критический случай): Если линеаризованная система нейтрально устойчива, то для суждения о устойчивости требуется отдельное исследование системы.