Шпоры к экзамену / Лекции 2 / Курс лекций 8

ТФКП. 4 семестр. Логинов А.С. 2006 г. loginov_1999@mail.ru

Глава 8. Приложения.

§1 Гармонические функции.

Определение. Гармонической в области D функцией называется действительная функция u(x,y) обладающая в D непрерывными вторыми производными и удовлетворяющая уравнению

Теорема. Действительная и мнимая части однозначной аналитической функции в области D являются гармоническими в этой области функциями.

Имеем f(z)=u(x,y)+iv(x,y)

(CR)

Откуда и следует требуемое равенство.

Определение. Две гармонические функции, связанные условиями (CR) называются сопряженными.

§2 Комплексный потенциал

Рассмотрим плоское поле

Соленоидальное поле ( без источников и стоков, поток через замкнутую кривую равен нулю ) . Тогда для формы выполнены условия полного дифференциала , поэтому существует функция , для неё

(1)

Определение. Функцией тока плоского соленоидального поля называется дважды непрерывно дифференцируемая функция v, удовлетворяющая соотношениям (1).

Функция тока находится по формуле

1. Потенциальное ( безвихревое поле ) . В этом случае существует потенциал .

2. Поле и потенциальное и соленоидальное. В этом случае, как это следует из 1) и 2), выполнены условия

, (2),

которые являются условиями Коши-Римана для функции

f(z)=u(x,y)+iv(x,y).

Эта функция называется комплексным потенциалом данного поля. Отметим, что в плоском поле без источников и вихрей функция тока и потенциал являются гармоническими сопряженными функциями. Как это следует из 1)-2)

Для такого поля поток

3. Восстановления функции тока по потенциалу.

Если потенциал u является гармонической функцией, то форма –Qdx+Pdy является полным дифференциалом и функция тока v восстанавливается по формуле

Аналогичным образом может быть восстановлен потенциал u по функции тока v, если она гармонична.

§3 Операционное исчисление

Дана задача Коши

a_n0. (1)

Будем предполагать, что f(t) и x(t) вместе со всеми производными до n-го порядка являются оригиналами. Положим x(t)X(p), f(t)F(p). Из свойств преобразования Лапласа следует, что

Отсюда, применяя преобразование Лапласа к (1) получим

, или

.

Таким образом,

, находя оригинал x(t)X(p) для функции X(p), получим решение задачи Коши.

Таблица основных свойств преобразования Лапласа

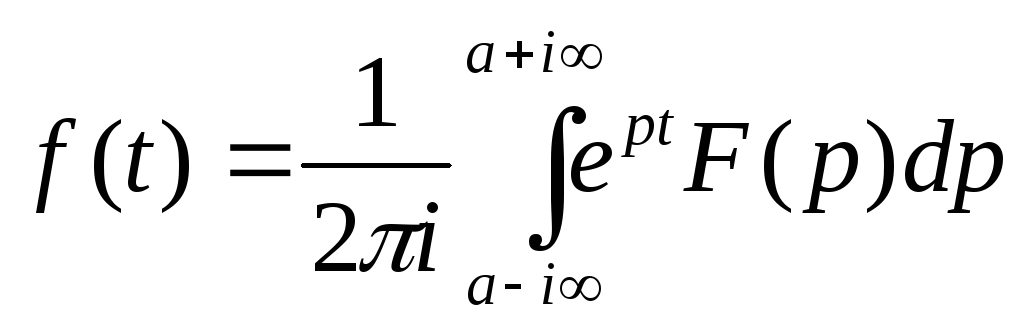
f(t)+g(t)F(p)+G(p)
0 ,	, f(t-)e-pF(p)
F(p-)etf(t)
f’(t)pF(p)-f(0),	f(n)(t)pnF(p)-pn-1f(0)-…-f(n-1)(0)

Таблица некоторых преобразований Лапласа

	Оригинал	Изображение
1	t (>-1)
2	e-t
3	e-t t (>-1)
4	sin t
5	cos t
6	tn sin t
7	tn cos t
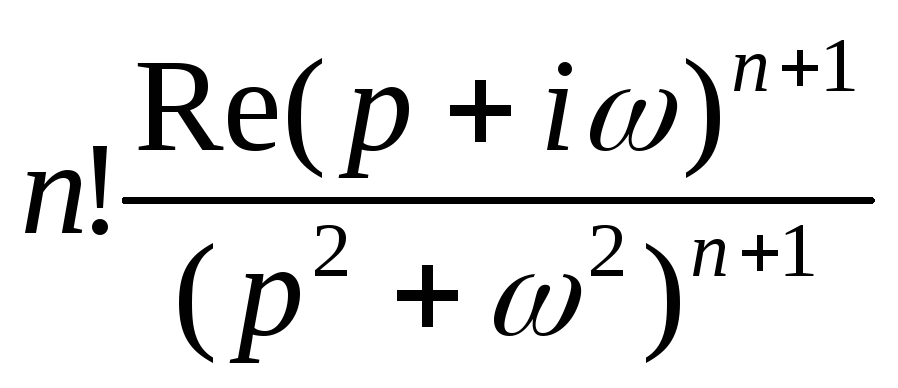
8	e-t sin (t+)
9	e-t cos (t+)
10	sh t
11	ch t
12
13
14
15
16
17
18
19
20

Пример 1. x’’+a²x=b sin at, общие начальные данные x₀, x₁,

, поэтому

Согласно 5 из таблицы ,

согласно 4 из таблицы ,

согласно 6 из таблицы , отсюда, используя свойство интегрирования оригинала, получим , откуда

Окончательно

Пример 2. x’’’+3x’’+3x’+x=1, нулевые начальные условия.

(p+1)³X(p)=1/p,. Откуда

Пример 3. x’’’+x=1, нулевые начальные условия.

Оригинал находим по второй теореме Хевисайда

Пример 3. x’’’+x=1, нулевые начальные условия.

,

По второй теореме Хевисайда

Пример 4. , нулевые условия. Используя 4 из таблицы, получим . По второй теореме Хевисайда

=

Пример 5. x’’+²x=a[H(t)-H(t-b)], нулевые начальные условия.

, по второй теореме Хевисайда

Свойство запаздывания дает

Окончательно

Пример 7.

x’+ax=f(t), нулевые условия

ТФКП. 4 семестр. Логинов А.С. 2006 г. loginov_1999@mail.ru