Метод множителей Лагранжа.
Метод неопределенных множителей Лагранжа. Если система функций уравнений (2) неразрешима, либо ее решение затруднительно для вас, используют более универсальный способ – метод неопределенных множителей Лагранжа. Идея та же – переход от условного экстремума к безусловному.
L=f+1F1+2F2+…+mFm (4)
Функция Лагранжа.
Теперь находим экстремум этой функции. Здесь 1, 2,…n –множители Лагранжа.
Предположим, что функция дифференцируема
L(u1,u2,…um,x1,x2,…,xn,1,2,…n)
Необходимые условия экстремума:
Необходимые
условия экстремума
Эта система содержит u+2m уравнений и u+2m переменных.
Мо(
о(
Для полученных точек проверяем достаточное условие экстремума.
Определение числового ряда, частичной суммы, сходящегося ряда.
Рассмотрим производную числовую последовательность а1, а2,….аn, …
Формально из элементов этой последовательности составим сумму
а1+а2+а….+аn=
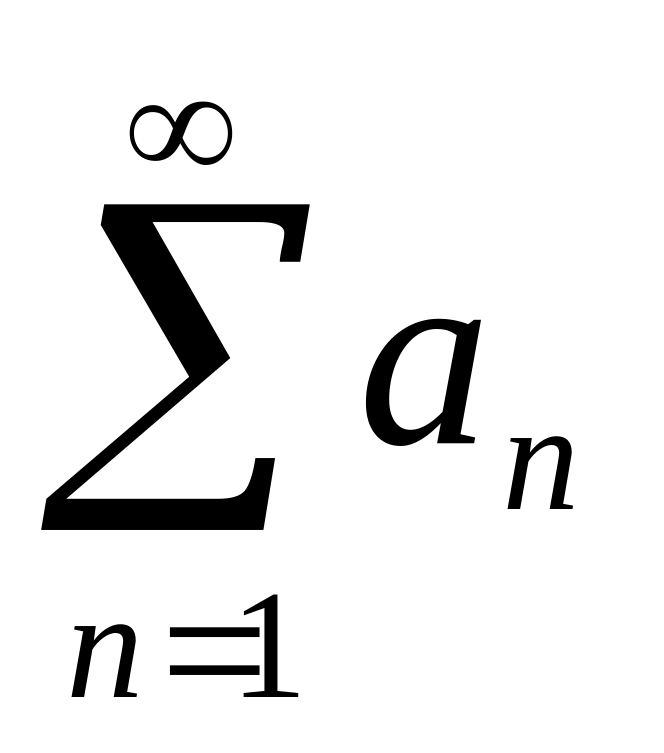
Такую сумму принято называть числовым рядом или просто рядом а1,а2,…аn, … элементы члены ряда
An – общий член ряда
Сумма
первых n членов ряда
называется частичной суммой n-переменных
Свойства сходящихся числовых рядов.
Необходимое условие сходимости числового ряда. Сходимость гармонического ряда.
Необходимое и достаточное условие сходимости ряда с неотрицательными членами.
Признак сравнения.
Признак Даламбера.
Интегральный признак Коши.
Знакочередующийся ряд. Признак Лейбница.
Знакопеременные ряды, их сходимость.
Степенные ряды.
Теорема Абеля.
Теорема об интервале сходимости степенного ряда.
Теорема о радиусе сходимости степенного ряда