§ 4. Основні положення вибіркового спостереження

При вибірковому спостереженні можуть виникати помилки реєст­рації і похибки вибірки (репрезентативності).

Помилки реєстрації, як і при суцільному статистичному спос­тереженні, являють собою розбіжність між зафіксованими даними в процесі спостереження і дійсними даними. Вони можуть бути випадковими і систематичними. Як правило, помилки реєстрації при вибірковому спостереженні трапляються рідко, тому що знач­но менший обсяг роботи припадає на одного реєстратора, самі реє­стратори завжди більш кваліфіковані, ніж при проведенні суціль­ного спостереження.

Як уже відзначалося, похибки репрезентативності притаманні будь-якому вибірковому спостереженню. Завдання організації пра­вильного проведення вибіркового спостереження — це вибір такої похибки репрезентативності, яка б задовольняла дослідника при даному спостереженні.

Зупинимося на основних термінах вибіркового спостереження. Основні поняття: генеральна і вибіркова сукупності. Генеральна су­купність — це вся сукупність одиниць, з якої проводиться відбір частини одиниць для вибіркового спостереження. Відібрана в пев­ний спосіб частина генеральної сукупності для вибіркового спосте­реження називається вибірковою сукупністю. Узагальнюючі показ­ники генеральної сукупності називаються генеральними, а відповідні показники вибіркової сукупності — вибірковими. Позначення показників генеральної та вибіркової сукупностей на­ведено втабл.13.

Таблиця 13 Позначення показників генеральної та вибіркової сукупності

Показник	Позначення
	у генеральній сукупності	у вибірковій сукупності
Кількість одиниць	N	п
Середнє значення ознаки	х	х
Частина одиниць, що мають дану ознаку	Р	\У
Частина одиниць, що не мають даної ознаки	^=1-р	1-У/

. Переваги вибіркового спостереження перед суцільним реалізу­ються лише при додержанні наукових принципів його організації і проведення, насамперед неупередженого, випадкового відбору оди­ниць для спостереження. Вибіркова сукупність повинна повністю відтворювати склад генеральної сукупності. Принцип випадковості відбору забезпечує всім одиницям генеральної сукупності рівні можливості потрапити у вибіркову сукупність.

При проведенні вибіркового спостереження слід спиратися на знання закону великих чисел і теорії імовірності. Але незалежно від того, яким чином проводився відбір одиниць сукупності, завжди будуть розбіжності між характеристиками генеральної і вибіркової сукупностей, пов'язані із сутністю вибіркового методу. Частина завжди відрізняється від цілого. Розбіжності між показниками ге­неральної і вибіркової сукупностей називаються похибками репре­зентативності. Існування їх пояснюється тим, що вибіркова су-

купність не зовсім точно відображає склад генеральної сукупності. Середня в генеральній сукупності відрізняється від середньої у ви­бірковій сукупності на величину похибки репрезентативності:

де Д (дельта) — похибка репрезентативності.

Наприклад, після проведення вибіркового спостереження з'я­сувалось, що середній вік рецидивістів дорівнює 32 рокам (х). Розрахована похибка репрезентативності (А) становить +5%, інак­ше кажучи — 1,6 роки (32х5%, або 32 х 0,05 = 1,6). Відповідно до наведеної формули середній вік рецидивістів у всій сукупності (32,0 ± 1,6) коливатиметься в межах від 30,4 до 33,6 років. Таким чином, ми вирішили головне завдання вибіркового спостереження — за здобутими нами вибірковими показниками (одержаними внаслідок проведеного дослідження) з'ясувати, чому дорівнюватимуть відповідні показники генеральної сукупності, які нам невідомі.

Згідно з теоремою Чебишева з уточненнями Ляпунова в мате­матиці було доведено, що при достатньо великій кількості обсте­жених одиниць сукупності середня величина досліджуваної озна­ки у вибірковій сукупності відрізнятиметься від середньої величи­ни в генеральній сукупності на величину

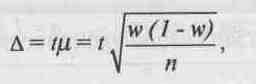
де Д (дельта) — гранична похибка вибірки, тобто похибка репрезентативності; р- (мю) — середня похибка вибірки; / — ко­ефіцієнт, що залежіть від імовірності, з якою можна гарантувати певний розмір похибки репрезентативності. Якщо / = 0, то імовірність також дорівнює 0; якщо 1= 0,5, то імовірність дорівнює 0,383, або 38,3%; якщо ї= 1, то імовірність дорівнює 0,683, або 68,3%; якщо ї= 2, то імовірність дорівнює 0,954, або 95,4%; якщо /= З, то імовірність дорівнює 0,997, або 99,7 %; якщо 1= 4, то імовірність" становить 0,999936 і т.под. При цьому слід враховувати, що даний коефіцієнт може приймати не тільки цілі числа, а й дробові значен­ня (інші умовні позначення містяться у табл. 13).

Із наведеної формули випливає, що похибка репрезентативності залежить від багатьох чинників: імовірності, з якою ми бажаємо одержати результат; кількості одиниць вибіркової сукупності (чим менше одиниць складатиме вибіркова сукупність, тим більше буде ;

похибка репрезентативності, і навпаки); однорідності досліджува­ної сукупності (чим більш різнорідною є сукупність, тим більше буде похибка репрезентативності) і від способу відбору одиниць у вибіркову сукупність.

Як правило, при вибірковому спостереженні перед дослідником для успішного його проведення необхідно поставити два взаємопо­в'язаних завдання: 1) визначення необхідної кількості одиниць ви­біркової сукупності, тобто скільки одиниць обстежуватиметься; та 2) розрахунок похибки репрезентативності з встановленим рівнем імо­вірності, тобто межі можливих відхилень вибіркового показника від відповідного показника в генеральній сукупності.

Багаторічна практика свідчить про те, що довірча імовірність 95,4 % (для / = 2) є оптимальною для більшості розрахунків у різних галузях господарства, тим більше для правових явищ. Тому для по­легшення досить громіздких розрахунків похибки вибіркового спо­стереження існують спеціальні таблиці, застосовуючи які можна визначити або величину похибки репрезентативності при певній кількості спостережень з довірчою імовірністю 95,4% (табл. 14), або кількість вибіркових спостережень при заданій величині похибки репрезентативності з довірчою імовірністю 95,4 % (табл. 15) без ви­користання вищенаведених формул. Застосування таблиць (14 або

Таблиця 14 Величина похибки вибірки при даній кількості спостережень

ї	• • " '
	Величина показника, %	Кількість спостережень
		100	200	300	400	500	600	700	800	900	1000
	5(95)	4,4	3,1	2,8	2,5	1,9	1,8	1,6	1,5	1,4	1,4
	10 (90)	6,0	4,3	3,5	3,0	2,7	2,5	2,3	2,1	2,0	1,9
	15(85)	7,2	5,1	4,1	3,6	3,2	2,9	2,7	2,5	2,4	2,3
	20 (80)	8,0	5,7	4,6	4,0	3,6	3,3	3,0	2,8	2,7	2,5
	25 (75)	8,7	6,2	5,0	4,3	3,9	3.5	3,3	3,1	2,9	2,7
	30 (70)	9,2	6,5	5,3	4,6	4,1	3,7	3,5	3,2	3,1	2,9
	35 (65)	9,6	6,8	5,5	4,8	4,3	3,9	3,6	3,4	3,2	3,0
	40 (60)	9,9	7,0	5,6	4,9	4,4	4,0	3,7	3,5	3,3	3,1
	45 (55)	10,0	7,1	5,7	5,0	4,5	4,1	3,8	3,5	3,3	3,1
	50	10,0	7,1	5,8	5.0	4,5	4,1	3,8	3.5	3,3	3,2

15) значно спрощує розрахунки і дає змогу швидше одержати ре­зультати. Вперше в навчальній літературі з правової статистики аналогічні таблиці було наведено у підручнику С. Остроумова «Со-ветская судебная статистика» (М., 1970).

Таблиця 14 дає можливість відповісти на питання, яку мінімаль­ну кількість одиниць сукупності необхідно включити до вибірко­вої сукупності, щоб очікуваний результат похибки репрезентатив­ності коливався в установлених межах.

На підставі даних, наведених у табл. 14, видно, що чим більше одиниць потрапляє до вибіркової сукупності, тим менше буде мож­ливою похибка вибірки, і навпаки. Це зрозуміло, бо при значному збільшенні одиниць, які потрапили до вибіркової сукупності, ми проводитиме суцільне спостереження.

Як можна і треба користуватися табл. 14? Наприклад, припус­тимо, що на основі обстеження 200 осіб, яких засуджено за тяжкі насильницькі злочини, було встановлено, що 65% з них вчинено в стані алкогольного сп'яніння. Нас цікавить, наскільки достовірним є цей результат, тобто в яких межах коливається дане значення в усій генеральній сукупності.

Заданими табл. 14 визначаємо, що на перетині горизонтального рядка з числом 65 з вертикальною другою графою з числом 200 зна­ходиться число 6,8. Це означає, що частка засуджених, що вчини­ли тяжкі насильницькі злочини в стані сп'яніння, може коливати­ся в межах від 58,2 % до 71,8 % (65% ± 6,8 %).

Якщо табл. 14 відсутня, то в цьому випадку всі розрахунки необхідно проводити на базі раніше наведеної формули (с. 212). Так, для приклада, який наведено і обчислено за допомогою табл. 14, де і = 2; и¹ = 0,65; п = 200, ми одержимо похибку ре­презентативності внаслідок такого розрахунку:

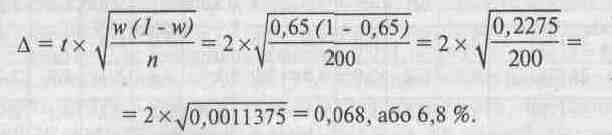
У конкретно-правових дослідженнях, як правило, відсоток по­хибки середнього значення задається самим дослідником на основі програми спостереження і відповідно до даних раніш проведених досліджень. Як правило, вважається допустимою гранична похиб­ка вибірки (похибка репрезентативності) в межах 3 — 5 %.

Якщо допустити похибку вдвічі більшу, то обсяг вибірки можна зменшити в чотири рази, і навпаки, якщо необхідно зменшити по­хибку вибірки вдвічі, то обсяг вибірки треба збільшити в чотири рази.

Слід звернути увагу на те, що табл. 14 побудовано для власне випадкового способу відбору одиниць у вибіркову сукупність, тому її з більшим ступенем вірогідності можна використовувати при ме­ханічному і типовому способах відбору одиниць у вибіркову су­купність. При серійному (гніздовому) способі відбору одиниць у вибірку використовувати дані, наведені в таблицях 14 і 15, не мож­на. (Більш докладно способи відбору одиниць у вибіркову сукуп­ність викладено в наступному підрозділі цього розділу підручника.)

Найважливіше завдання при проведенні вибіркового дослід­ження правових явищ — це визначення репрезентативного обсягу вибіркового спостереження, тобто скільки необхідно проаналізу­вати одиниць з генеральної сукупності, щоб одержана випадкова похибка середнього значення досліджуваної ознаки не перевершу­вала визначеної величини похибки репрезентативності з достат­ньою імовірністю.

Спираючись на математичні теореми закону великих чисел, можна встановити, що при зменшенні обсягу вибірки в декілька квадратів разів похибка середнього значення збільшується в стільки ж разів, і навпаки, зменшення похибки середнього значення вибір­ки в декілька разів призводить до збільшення обсягу вибірки в стільки ж квадратів разів. Отже, визначення величини похибки се­реднього значення ознаки для встановлення обсягу вибірки є дуже важливим.

При практичному застосуванні формул дослідник завжди сти­кається з тим, що необхідні дані про коливання ознаки в гене­ральній сукупності. Як правило, на практиці для визначення обсягу вибірки вдаються до даних попередніх досліджень або проводять так звані пробні обстеження і на їх основі визначають орієнтовні розміри коливання ознаки.

Взагалі слід пам'ятати, що головне при організації вибіркового спостереження — це доведення його обсягу до допустимого мініму­му. При цьому не слід прагнути до надмірного зменшення меж по­хибки вибірки, бо це може призвести до невиправданого збільшен­ня обсягу вибірки і, отже, до підвищення витрат на проведення вибіркового спостереження. В той же час не можна і надмірно збільшувати розмір похибки репрезентативності, оскільки в цьому випадку хоча і відбудеться зменшення обсягу вибіркової сукуп-

ності, але це призведе до погіршення достовірності одержаних ре­зультатів.

Наведемо приклад визначення чисельності вибірки на основі табл. 15. Припустимо, що величина досліджуваного показника до­рівнює 40 % (частка (питома вага) тяжких злочинів в області), а похибка репрезентативності, яку вважаємо допустимою при дано­му дослідженні, не повинна перевищувати ± 4 %. За табл. 15 визна­чаємо, що мінімальний обсяг вибіркової сукупності повинен склас­ти 600. Отже, щоб наше вибіркове дослідження було репрезентатив­ним з довірчою імовірністю в 95,4 % за наших вихідних даних, нам необхідно обстежити як мінімум 600 засуджених.

Таблиця 15

Кількість спостережень, які необхідно провести при заданій похибці репрезентативності (обсяг вибіркової сукупності)

Величина показника,%	Величина похибки репрезентативності, %
	1	2	3	4	5	10
10	3600	900	400	230	150	37
20	6400	1600	710	400	260	65
40	9600	2400	1070	600	390	97
45	9900	2500	1100	620	400	100
55	9900	2500	1100	620	400	100
65	9100	2300	1010	570	370	92
70,	8400	2100	930	530	340	85
80	6400	1600	710	400	260	65

Обсяг вибіркової сукупності також обчислюється на базі раніш наведеної формули (якщо відсутня табл. 15). Формула для встанов­лення обсягу вибіркової сукупності шляхом її нескладного перетво­рення матиме такий вигляд:

де л — обсяг вибіркової сукупності; v— частина одиниць, які мають дану ознаку; / — коефіцієнт, квадрат якого гарантує вірогідність довірчого інтервалу в 95,4 %; Д — похибка репрезента­тивності.

За даними, обчисленими на базі табл. 15, де І² = 4; v = 40 % (0,40); Д² = ± 4 % (± 0,04), у вибіркову сукупність необхідно взяти 600 одиниць, щоб із імовірністю 95,4% можна було стверджувати, що похибка репрезентативності при обчисленні частки сукупності не відхилятиметься більше ніж на ± 4%, якщо відомо, що значен­ня частки у сукупності досягає 40%, тобто за наведеною формулою

Якщо внаслідок обчислення ми одержимо обсяг вибіркової су­купності у вигляді не цілого числа, то необхідно прийняти її у виг­ляді найбільшого числа, наприклад, щоб з імовірністю 95,4% можна було стверджувати, що похибка репрезентативності при обчисленні частки сукупності не відхилятиметься більше ніж на ± 4%. Значен­ня частки у сукупності досягає 25%, тобто за наведеною формулою

жали, що обсяг вибіркової сукупності повинен становити 468,75 одиниць (тим більше, що аналогічні дані в таблицях 14 і 15 відсутні), отже, у вибіркову сукупність необхідно взяти 470—500 одиниць, щоб якість нашого вибіркого спостереження не погіршилася.

У більшості випадків при вибіркових дослідженнях дані аналі­зуються і збирають не по одному, а по декількох ознаках одночас­но. У цьому випадку необхідний обсяг вибіркової сукупності виз­начається по кожній з цих ознак, а потім для дослідження прий­мається максимальна величина по одній з найбільш істотних ознак.

За наявності якісної сукупності альтернативних ознак (подія може або настати, або не настати), якщо невідома реальна величи­на коливання ознаки, його величина приймається рівнозначною 50% (більш докладно це відображено в розділі VIII підручника).