Свойства математического ожидания

.

.

.

Свойства дисперсии случайной величины

1. Дисперсия постоянной величины С равна нулю .

2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат .

3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин

.

4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий

.

3. Равномерный закон распределения и его числовые характеристики. (док-ва в к)

Непрерывная случайная величина Х имеет равномерный закон распределения на отрезке , если ее плотность вероятности р(х) постоянна на этом отрезке и равна нулю вне его, т.е.

Функция распределения случайной величины Х, распределенной по равномерному закону, есть

Математическое ожидание дисперсия а среднее квадратическое отклонение .

3. Показательный закон распределения и его числовые характеристики.

Непрерывная случайная величина Х имеет показательный (экспоненциальный) закон распределения с параметром λ, если ее плотность вероятности имеет вид

Функция распределения случайной величины, распределенной по показательному закону, равна

Кривая распределения р(х) и график функции распределения :

Для случайной величины, распределенной по показательному закону

; .

Вероятность попадания в интервал непрерывной случайной величины Х, распределенной по показательному закону

.

Замечание. Показательный закон распределения вероятностей встречается во многих задачах, связанных с простейшим потоком событий. Под потоком событий понимают последовательность событий, наступающих одно за другим в случайные моменты. Например, поток вызовов на телефонной станции, поток заявок в системе массового обслуживания и др.

3. Нормальный закон распределения. Влияние параметров распределения на вид нормальной кривой.

Неслучайная величина Х имеет нормальный закон распределения (закон Гаусса) с параметрами а и , если ее плотность вероятности имеет вид

.

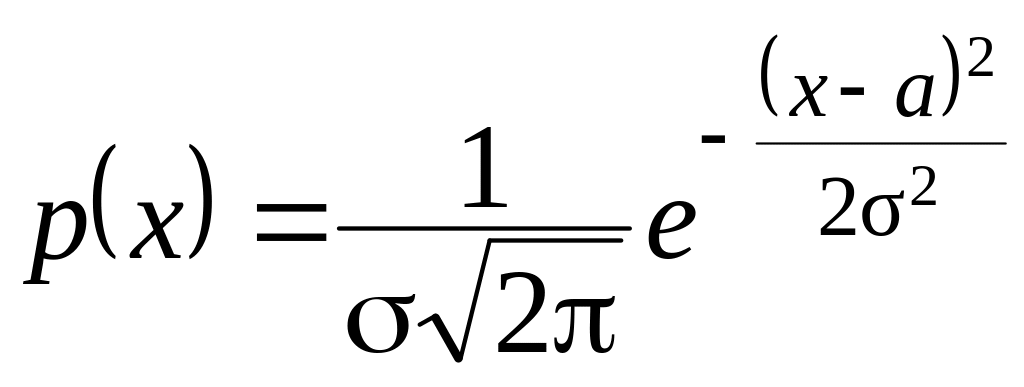К ривую нормального закона распределения называют нормальной или гауссовой кривой.

Нормальная кривая р(х) с параметрами а и , т.е. , и график функции распределения случайной величины Х, имеющей нормальный закон:

Нормальная кривая симметрична относительно прямой х = а, имеет максимум в точке х = а, равный , и две точки перегиба

с ординатой .

3. Числовые характеристики случайной величины, имеющей нормальное распределение.

Для случайной величины, распределенной по нормальному закону, , .

Функция распределения случайной величины Х, распределенной по нормальному закону, выражается через функцию Лапласа Ф(х) по формуле

, где .

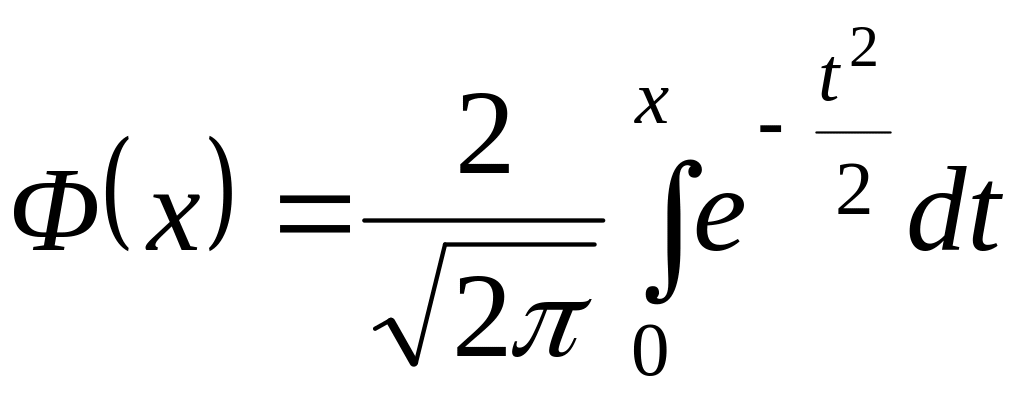3. Вероятность попадания в заданный интервал нормально распределенной случайной величины. Вероятность заданного отклонения. Правило трех сигм.

Вероятность попадания значений нормальной случайной величины Х в интервал определяется формулой

.

Вероятность того, что отклонение случайной величины Х, распределенной по нормальному закону, от математического ожидания а не превысит величину (по абсолютной величине), равна .

«Правило трех сигм»: если случайная величина Х имеет нормальный закон распределения с параметрами а и т.е. , то практически достоверно, что ее значения заключены в интервале

.

Асимметрия нормального распределения А = 0; эксцесс нормального распределения Е = 0.