31) Показатели качества регрессии.

Система показателей качества Регрессии.

• Показатели качества параметров Регрессии :

1. Стандартные ошибки оценок (анализ точности

определения оценок).

2. Значения t-статистик (проверка гипотез

относительно коэффициентов регрессии).

3. Интервальные оценки коэффициентов

линейного уравнения регрессии.

4. Доверительные области для зависимой

переменной.

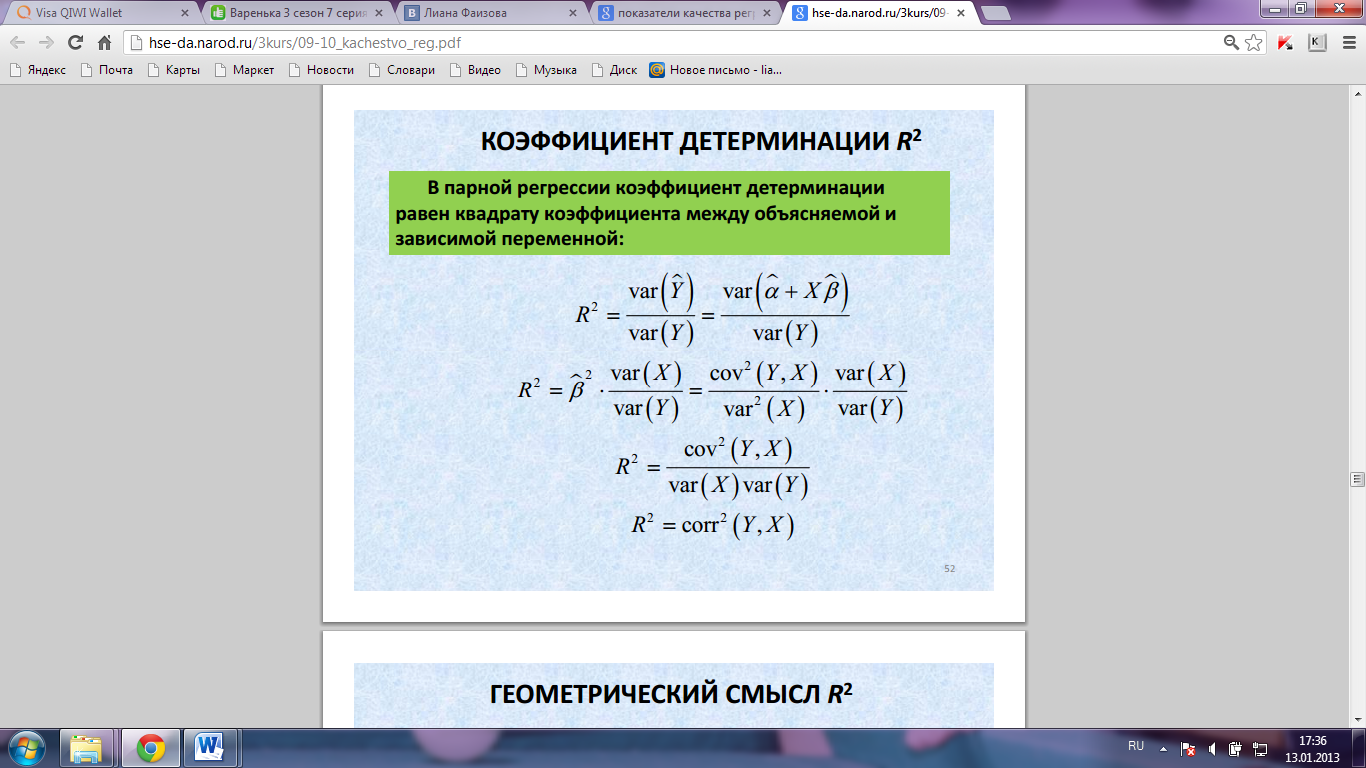
• Показатели качества уравнения

регрессии в целом:

Суть проверки общего качества уравнения регрессии –

оценить насколько хорошо эмпирическое уравнение

регрессии согласуется со статистическими данными.

32) Парная регрессия и корреляция как частный случай множественной регрессии и корреляции

По форме проявления взаимосвязей выделяют функциональную (полную) икорреляционную (неполную) связи. Корреляционная связь является частным случаем стохастической связи. В первом случае величине факторного признака строго соответствует одно или несколько значений функции. 

Функциональные связи характеризуются полным соот­ветствием между изменением факторного признака и изменением результативной величины и каждому значению признака-фактора соответствуют вполне определенные значения результативного признака. Функциональная зависимость может связывать резуль­тативный признак с одним или несколькими факторными признаками. Функциональную связь можно представить уравнением: y_i = f(x_i), где:

• f(x_i)-известная функция связи результативного и факторного признаков;

• y_i-результативный признак ( i = 1, … , n);

• x_i -факторный признак.

Стохастическая связь – это связь между величинами, при которой одна из них, случайная величина у, реагирует на изменение другой величины х или других величинх₁,х₂ …х_n (случайных или неслучайных) изменением закона распределения. Это обуславливается тем, что зависимая переменная (результативный признак), кроме рассматриваемых независимых, подвержена влиянию ряда неучтенных или неконтролируемых (случайных) факторов, а также некоторых неизбежных ошибокизмерения переменных. Поскольку значения зависимой переменной подвержены случайному разбросу, они не могут быть предсказаны с достаточной точностью, а только указаны с определенной вероятностью.

Корреляционная связь (которую также называют неполной, или статистической) проявляется в среднем, для массовых наблюдений, когда заданным значениям зависимой переменной соответствует некоторый ряд вероятных значений независимой переменной. Объяснение тому – сложность взаимосвязей между анализируемыми факторами, на взаимодействие которых влияют неучтенные случайные величины. Поэтому связь между признаками проявляется лишь в среднем, в массе случаев. При корреляционной связи каждому значению аргумента соответствуют случайно распределенные в некотором интервале значения функции.

В корреляционных связях между изменением фактор­ного и результативного признака нет полного соответствия. Одновременное воз­действие на изучаемый признак большого количества самых разнообразных факторов приводит к тому, что одному и тому же значению признака-фактора соответствует целое распределение значений результативного признака, поскольку в каждом конкрет­ном случае прочие факторные признаки могут изменять силу и направленность своего воздействия.

При сравнении функциональных и корреляционных зависи­мостей следует иметь в виду, что при наличии функциональной зависимости между признаками можно, зная величину факторного признака, точно определить величину результативного признака. При наличии же корреляционной зависимости устанавливается лишь тенденция изменения результативного признака при изме­нении величины факторного признака. В отличие от жесткости функциональной связи, корреляционные связи характеризуются множеством причин и следствий, и устанавливаются лишь их тен­денции.

По направлению связи бывают прямыми, когда зависимая переменная растет с увеличением факторного признака, и обратными, при которых рост последнего сопровождается уменьшением функции. Такие связи также можно назвать соответственно положительными и отрицательными.

По силе различаются сильные и слабые связи, либо полное их отсутствие. Эта формальная характеристика выражается конкретными величинами и интерпретируется в соответствии с общепринятыми критериями силы связи для конкретных показателей.

33) Вывод формул для параметров парного линейного корреляционного уравнения

Уравнение парной линейной корреляционной связи называется уравнением парной регрессии и имеет вид:

у = а + bх,                                                                                                       

где   у - среднее значение результативного признака> при определенном значении факторного признака х;

а - свободный член уравнения;

b - коэффициент регрессии, измеряющий среднее отношение отклонения результативного признака от его средней величины к отклонению факторного признака от его средней величины на одну единицу его измерения - вариация у, приходящаяся на единицу вариации х.

Уравнение (8.4) определяется по данным о значениях признаков х и у в изучаемой совокупности, состоящей из п единиц. Параметры уравнения а и b находятся методом наименьших квадратов (МНК).

Исходное условие МНК для прямой линии имеет вид:

34) Интерпретация и применение корреляционного уравнения (уравнения регрессии).

Применение корреляционного анализа позволяет решить следующие задачи:

• определить изменение результативного показателя под воздействием одного или нескольких факторов (в абсолютном измерении), т.е. определить, на сколько единиц изменяется величина результативного показателя при изменении факторного на единицу;

• установить относительную степень зависимости результативного показателя от каждого фактора.

Первая задача решается путем подбора и обоснования соответствующего типа уравнения связи и нахождения его параметров. Уравнение связи обосновывается с помощью графиков, аналитических группировок и т.д.

Зависимость результативного показателя от определяющих его факторов можно выразить уравнениемпарной и множественной регрессии. При прямолинейной форме она имеет следующий вид:

1. уравнение парной регрессии:

2. уравнение множественной регрессии:

• a – свободный член уравнения

• x₁,x₂…x_n – факторы, определяющие уровень изучаемого результативного показателя; 

• b₁,b₂…b_n – коэффициенты регрессии при факторных показателях, характеризующие уровень влияния каждого фактора на результативный показатель в абсолютном выражении. 

Расчет уравнения связи сводится к определению параметров а, b, с. В соответствии с требованиями метода наименьших квадратов для определения параметров   необходимо решить следующие системы уравнений.

1. В случае прямолинейной зависимости:

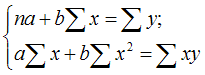
2. В случае криволинейной зависимости между изучаемыми явлениями, когда при увеличении одного показателя, значения другого возрастают до определенного уровня, а потом начинают снижаться (например, зависимость производительности труда рабочих от их возраста), то для записи такой зависимости лучше всего подходит парабола второго порядка:

3. В случае криволинейной зависимости, когда при увеличении одной переменной значения другой увеличиваются до определенного уровня, а потом прирост снижается, например зависимость урожайности от количества внесенного удобрения, продуктивности животных от уровня их кормления, себестоимости единицы продукции от объема ее производства и т.д. Такую зависимость лучше описывает  гипербола:

При более сложном характере зависимости между изучаемыми явлениями используются более сложные полиномы (третьего, четвертого порядка и т.д.), степенные, показательные и другие функции.

35) Измерение тесноты связи. Коэффициент корреляции.

Корреля́ция(от лат. correlatio), (корреляционная зависимость) — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин.^[1] Математической мерой корреляции двух случайных величин служит корреляционное отношение  ^[2], либо коэффициент корреляции   (или  )^[1]. В случае, если изменение одной случайной величины не ведёт к закономерному изменению другой случайной величины, но приводит к изменению другой статистической характеристики данной случайной величины, то подобная связь не считается корреляционной, хотя и является статистической^[3].

Впервые в научный оборот термин «корреляция» ввёл французский палеонтолог Жорж Кювье в XVIII веке. Он разработал «закон корреляции» частей и органов живых существ, с помощью которого можно восстановить облик ископаемого животного, имея в распоряжении лишь часть его останков. В статистике слово «корреляция» первым стал использовать английский биолог и статистик Фрэнсис Гальтон в конце XIX века.^[4]

Некоторые виды коэффициентов корреляции могут быть положительными или отрицательными. В первом случае предполагается, что мы можем определить только наличие или отсутствие связи, а во втором — также и её направление. Если предполагается, что на значениях переменных задано отношение строгого порядка, то отрицательная корреляция — корреляция, при которой увеличение одной переменной связано с уменьшением другой. При этом коэффициент корреляции будет отрицательным. Положительная корреляция в таких условиях — это такая связь, при которой увеличение одной переменной связано с увеличением другой переменной. Возможна также ситуация отсутствия статистической взаимосвязи — например, для независимых случайных величин.

Корреляционный анализ — метод обработки статистических данных, с помощью которого измеряется теснота связи между двумя или более переменными. Корреляционный анализ тесно связан с регрессионным анализом (также часто встречается термин «корреляционно-регрессионный анализ», который является более общим статистическим понятием), с его помощью определяют необходимость включения тех или иных факторов в уравнение множественной регрессии, а также оценивают полученное уравнение регрессии на соответствие выявленным связям (используя коэффициент детерминации).

Множество корреляционных полей. Распределения значений (x, y) с соответствующими коэффициентами корреляций для каждого из них. Коэффициент корреляции отражает «зашумлённость» линейной зависимости (верхняя строка), но не описывает наклон линейной зависимости (средняя строка), и совсем не подходит для описания сложных, нелинейных зависимостей (нижняя строка). Для распределения, показанного в центре рисунка, коэффициент корреляции не определен, так как дисперсия y равна нулю.

1. Применение возможно при наличии достаточного количества наблюдений для изучения. На практике считается, что число наблюдений должно быть не менее, чем в 5-6 раз превышать число факторов (также встречается рекомендация использовать пропорцию не менее, чем в 10 раз превышающую количество факторов). В случае, если число наблюдений превышает количество факторов в десятки раз, в действие вступает закон больших чисел, который обеспечивает взаимопогашение случайных колебаний.^[13]

2. Необходимо, чтобы совокупность значений всех факторных и результативного признаков подчиняласьмногомерному нормальному распределению. В случае, если объём совокупности недостаточен для проведения формального тестирования на нормальность распределения, то закон распределения определяется визуально на основе корреляционного поля. Если в расположении точек на этом поле наблюдается линейная тенденция, то можно предположить, что совокупность исходных данных подчиняется нормальному закону распределения.^[14].

3. Исходная совокупность значений должна быть качественно однородной.^[13]

4. Сам по себе факт корреляционной зависимости не даёт основания утверждать, что одна из переменных предшествует или является причиной изменений, или то, что переменные вообще причинно связаны между собой, а не наблюдается действие третьего фактора.^[5]