Так как свободная поверхность, как поверхность равного давления, должна быть нормальна к указанной равнодействующей, то она в данном случае представит собой уже не горизонтальную плоскость, а наклонную, составляющую угол α с горизонтом. Учитывая, что величина этого угла зависит только от ускорений, приходим к выводу, что положение свободной поверхности не будет зависеть от рода находящейся в цистерне жидкости. Любая другая поверхность уровня в жидкости также будет плоскостью, наклоненной к горизонту под углом α. Если бы движение цистерны было не равноускоренным, а равнозамедленным, направление ускорения изменилось бы на обратное, и наклон свободной поверхности обратился бы в другую сторону.

В качестве второго примера рассмотрим часто встречающийся в практике случай относительного покоя жидкости во вращающихся сосудах (например, в сепараторах и центрифугах, применяемых для разделения жидкостей).

В этом случае на любую частицу жидкости при ее относительном равновесии действуют массовые силы: сила тяжести G = mg и центробежная сила P_u = mω²r, где r - расстояние частицы от оси вращения, а ω - угловая скорость вращения сосуда.

Поверхность жидкости также должна быть нормальна в каждой точке к равнодействующей этих сил R и представит собой параболоид вращения. Из чертежа находим

С другой стороны:

где z - координата рассматриваемой точки. Таким образом, получаем:

откуда

или после интегрирования

В точке пересечения кривой АОВ с осью вращения r = 0, z = h = C, поэтому окончательно будем иметь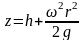

Т.е. кривая АОВ является параболой, а свободная поверхность жидкости параболоидом. Такую же форму имеют и другие поверхности уровня.

Для определения закона изменения давления во вращающейся жидкости в функции радиуса и высоты выделим вертикальный цилиндрический объем

жидкости с основанием в виде элементарной горизонтальной площадки dS (точка М) на произвольном радиусе r и высоте z и запишем условие его равновесия в вертикальном направлении. Будем иметь

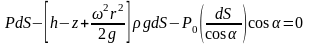
После сокращений получим

Это значит, что давление возрастает пропорционально радиусу r и уменьшается пропорционально высоте z.

21. Законы кинематики и динамики жидкости, основные понятия и определения.

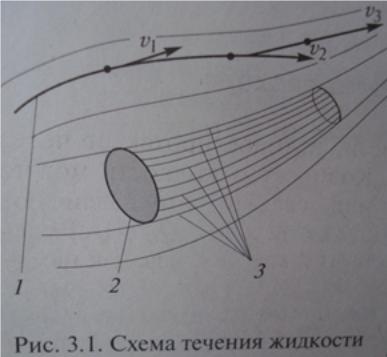
Идеальная жидкость – абсолютно невязкая жидкость. Течения жидкости может быть установившимся (все физические параметры в данной точке потока остаются неизменными во времени, например, истечение через отверстие в дне сосуда при постоянном уровне жидкости в сосуде) и неустановившимся (тоже истечение, но без поддержания постоянного уровня жидкости в сосуде). Линия тока (линия 1) – условная линия в потоке жидкости, проведённая так, что вектор скорости в любой её точке направлен по касательной. При установившемся течении линия тока совпадает с траекторией движения частицы жидкости. Линии тока не могут пересекаться, т.к. в любой точке потока при установившемся течении существует только одна скорость. Трубка тока – объединение линии 2, состоящей из бесконечного множества точек, и линий 3 (линий тока, проведённых из каждой такой точки). Т.к. ни одна линия тока не может пронизывать трубку тока, то ни одна частица жидкости не может проникнуть во внутрь или выйти из неё. Трубка тока при установившемся течении является непроницаемой стенкой для жидкости. Сечения потока (живые сечения) – поверхности, нормальные к линиям тока. Различают напорные и безнапорные течения жидкости. Напорными называют течения в закрытых руслах без свободной поверхности (например, в трубопроводах, гидромашинах), а безнапорными – течения со свободной поверхностью (в реках, открытых каналах).

22. Расход. Уравнение расхода жидкости.

Расход – количество ж-идкоси, которое протекает через данное сечение в единицу времени. Различают объёмный Q(м³/с), массовый Q_m(кг/с) и весовой Q_G (Н/с) расходы. Q_m = Q ; Q_G = Q_mg; Q_G = Q g.

Связь основных геометрических и кинематических параметров. При течении идеальной жидкости (а): 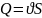, где – скорость жидкости, – площадь сечения. При течении реальной жидкости (б): 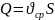, где – условная скорость, существующая в каком-то промежуточном слое потока реальной жидкости (лежит в пределах ). Из рисунка потока жидкости: Q₁=Q₂ , S₁ = S₂ (1). Уравнение (1) называют уравнением неразрывности или уравнением расхода; является законом сохранения вещества для потока жидкости, записанное при условии постоянства плотности жидкости в пределах рассматриваемого потока.

, ( – касательные напряжения). Т.к. и ( – градиент скорости, динамическая вязкость жидкости), то , где l – условный геометрический размер поперечного сечения потока. Таким образом, , для круглых труб , для напорных потоков с некруглыми сечениями ( - гидравлический диаметр: , где П – периметр сечения).

25. Основы гидродинамического подобия течения жидкости.

Суть методов моделирования физических процессов заключается в том, что при расчёте конкретной гидросистемы используются закономерности, полученные ранее при изучении подобных процессов в других гидросистемах. Эффективность методов моделирования во многом определяется правильностью подбора подобного физического процесса, т.е. решения вопроса: какие явления и в каких случаях можно считать подобными, а какие нет. Поэтому используют критерии подобия (безразмерные). Критериев подобия достаточно много.

1. Геометрическое подобие: подобие геометрических размеров в исходных точках; это подобие русел, по которым движется жидкость, в том числе их расположение относительно горизонта.

2. Кинематическое подобие: подобие скоростей в сходственных точках; признаками кинематического подобия двух геометрически подобных потоков могут являться одинаковые зоны распределения скоростей в сходственных сечениях.

3. Динамическое подобие: подобие сил (по величине и направлению), действующих на сходные объёмы. В потоках реальных жидкостей действуют различные силы, поэтому для сравнения берут силу инерции F_ин и сравнивают с ней какую-либо конкретную силу. Два потока динамически подобны, если полученные отношения одинаковы.

4. На практике используют частные критерии подобия. Критерий с использованием сил трения называют числом Рейнольдса: (это частный случай числа Ньютона: 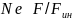). Два напорных потока динамически подобны, если в их сходственных сечениях одинаковы числа Рейнольдса.

Закон Рейнольдса: для обеспечения полного гидродинамического подобия двух геометрически подобных напорных потоков необходимо равенство чисел Рейнольдса, подсчитанных для любой пары сходственных сечений этих потоков.

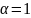– поток идеальной жидкости, .

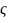, где – безразмерный коэф-т, определяющий потери в данном местном сопротивлении,

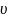– средняя скорость в трубопроводе, в котором установлено местное сопротивление,

– безразмерный коэффициент потерь на трение по длине (коэф-т Дарси).

24. Уравнение Бернулли для потока реальной жидкости.

Пусть поток реальной жидкости, обладающий вязкостью, движется в русле, ограниченном неподвижными стенками. Будем основываться на том, что уравнение Бернулли является законом сохранения энергии для движущейся жидкости. На первом этапе учтём неравномерность распределения скоростей по сечению потока, на втором – и потери энергии. Будем считать, что (справедливо только для плоских сечений). Полный напор сечения 1-1 струйки жидкости . Мощность струйки dN в сечении площадью dS: (Q_G = Q_m =Q ). Мощность всего потока: . 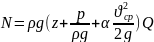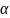После преобразований: , где – безразмерный коэффициент: . Этот коэффициент (Кориолиса) учитывает неравномерность распределения скорости потока жидкости в сечении реального потока (физический смысл: а – отношение действительной кинетической энергии реального потока в данном сечении к кинетической энергии того же потока в том же сечении, но посчитанной по средней скорости жидкости в данном сечении). . В реальных потоках из-за потерь при движении жидкости среднее значение полного напора в конечном сечении, поэтому или

(1) – уравнение Бернулли для потока реальной жидкости.

Энергетический смысл уравнения Бернулли (1): в потоке идеальной жидкости её полная удельная энергия в сечении есть величина постоянная. (1) – закон сохранения энергии для струйки идеальной жидкости.

23. Уравнение Бернулли для струйки идеальной жидкости.

Рассмотрим установившееся течение элементарной струйки идеальной жидкости, на которую действуют только силы тяжести. Выберем два сечения 1-1 и 2-2 и произвольную горизонтальную поверхность. Будем считать, что существует v₁ и v₂, действует давление р₁ и р₂ , центры тяжестей сечений располагаются на высоте z₁ . Пусть за dt участок струйки сдвинулся и занял положение, ограниченное 1’-1’ и 2’-2’. Тогда . Следовательно, равны массы ( ) и веса ( ). Тогда изменение кинетической энергии всего жидкого тела будет определяться разностью кинетических энергий выделенных объёмов: 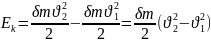. Работа сил тяжести: . Работа сил давления (работа положительной и отрицательной сил): . Выполнив следующие действия: 1) ; 2) разделив каждый член уравнения на вес ; 3) приняв, что получим (1).

и 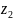– удельные энергии положения ж-ти в сечениях (нивелирные высоты); - удельные энергии давления (сжатия) жидкости в сечениях (пьезометрические высоты);

и - удельные потенциальные энергии жидкости в сечениях (гидростатические напоры);

и – удельные кинетические энергии жидкости в сечениях (скоростные напоры);

и – полные удельные энергии в каждом сечении струйки жидкости (полные напоры Н).

26. Режимы течения жидкости.

При наблюдении за движением жидкости в трубах и каналах, можно заметить, что в одном случае жидкость сохраняет определенный строй своих частиц, а в других - перемещаются бессистемно. На рис. 4.1 изображена установка, аналогичная той, на которой Рейнольдс производил свои опыты.

Установка состоит из резервуара А с водой, от которого отходит стеклянная труба В с краном С на конце, и сосуда D с водным раствором краски, которая может по трубке вводиться тонкой струйкой внутрь стеклянной трубы В.

Первый случай движения жидкости. Если немного приоткрыть кран С и дать возможность воде протекать в трубе с небольшой скоростью, а затем с помощью крана Е впустить краску в поток воды, то увидим, что введенная в трубу краска не будет перемешиваться с потоком воды. Струйка краски будет отчетливо видимой вдоль всей стеклянной трубы, что указывает на слоистый характер течения жидкости и на отсутствие перемешивания. Если при этом, если к трубе подсоединить пьезометр или трубку Пито, то они покажут неизменность давления и скорости по времени. Такой режим движения называется ламинарный.

Второй случай движения жидкости. При постепенном увеличении скорости течения воды в трубе путем открытия крана С картина течения вначале не

меняется, но затем при определенной скорости течения наступает быстрое ее изменение. Струйка краски по выходе из трубки начинает колебаться, затем размывается и перемешивается с потоком воды, причем становятся заметными вихреобразования и вращательное движение жидкости. Пьезометр и трубка Пито при этом покажут непрерывные пульсации давления и скорости в потоке воды. Такое течение называется турбулентным (рис.4.1, вверху).

Если уменьшить скорость потока, то восстановится ламинарное течение.

Ламинарным называется слоистое течение без перемешивания частиц жидкости и без пульсации скорости и давления. При ламинарном течении жидкости в прямой трубе постоянного сечения все линии тока направлены параллельно оси трубы, при этом отсутствуют поперечные перемещения частиц жидкости.

Турбулентным называется течение, сопровождающееся интенсивным перемешиванием жидкости с пульсациями скоростей и давлений. Наряду с основным продольным перемещением жидкости наблюдаются поперечные перемещения и вращательные движения отдельных объемов жидкости. Переход от ламинарного режима к турбулентному наблюдается при определенной скорости движения жидкости. Эта скорость называется критической v_кр.

Значение этой скорости прямо пропорционально кинематической вязкости жидкости и обратно пропорционально диаметру трубы.

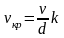
где ν – кинематическая вязкость; k - безразмерный коэффициент; d – внутренний диаметр трубы.

Входящий в эту формулу безразмерный коэффициент k, одинаков для всех жидкостей и газов, а также для любых диаметров труб. Этот коэффициент называется критическим числом Рейнольдса Re_кр и определяется следующим образом:

Для труб круглого сечения Re_кр примерно равно 2300.

Таким образом, критерий подобия Рейнольдса позволяет судить о режиме течения жидкости в трубе. При Re < Re_кр течение является ламинарным, а при Re > Re_кр течение является турбулентным. Точнее говоря, вполне развитое турбулентное течение в трубах устанавливается лишь при Re примерно равно 4000, а при Re = 2300…4000 имеет место переходная, критическая область.

Режим движения жидкости напрямую влияет на степень гидравлического сопротивления трубопроводов.