11. Гетероск-сть случайного возмущения. Причины. Последствия. Тест gq.

Гетеро-ть (неоднородность) - понятие математической статистики и эконометрии; означает ситуацию, когда дисперсия ошибки в уравнении регрессии изменяется от наблюдения к наблюдению. В этом случае приходится подвергать определенной модификации МНК (иначе возможны ошибочные выводы). Для обнаружения гетеро-ти обычно используют 3 теста, в которых делаются различные предположения о зависимости между дисперсией случайного члена и объясняющей переменной: тест ранговой корреляции Спирмена, тест Голдфельда - Квандта и тест Глейзера Доугерти. При малом объеме выборки для оценки гетеро-ти может использоваться метод Г-К. Данный тест используется для проверки такого типа гетероскедастичности, когда дисперсия остатков воз­растает пропорционально квадрату фактора. При этом делается предположение, что, случайная составляющая распределена нормально.

Последствия: истинная гетеро-ть не приводит к смещению оценок коэффициентов регрессии; гетеро-ть увеличивает дисперсию распределения оценок коэффициентов; гетеро-ть вызывает тенденцию к недооценке стандартных ошибок коэффициентов при использовании МНК.

Тест Г-К позволяет проконтролировать равенство дисперсий случайных возмущений.

Алгоритм теста:

1. сформировать служебную переменную p_i=|x_1i|+|x_2i|+…+|x_ki|

2. упорядочить уравнения наблюдений в порядке возрастания переменной p_i

3. разбить полученные уравнения примерно на 3 равные части

4. оценить модели по первой и последней частям уравнений наблюдений и вычислить для них ESS (дисперсии)

5. вычислить статистики GQ=ESS1/ESS2 и GQ^-1

6. найти значение Fкрит (через функцию FРАСПОБР)

7. сравнить полученные статистики с Fкрит. Если GQ<= Fкрит и GQ^-1<=Fкрит, то остаток в модели гомо-чен.

12. Двухшаговый метод наименьших квадратов для оценки параметров структурной формы модели

Выполним оценку структурных параметров уравнения системы ДМНК. Запишем уравнения наблюдений, с учетом условия нормализации, в следующем виде: 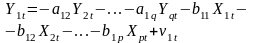, (10.31)

t=1,...,n, q – число эндогенных переменных, включенных в первое уравнение, p – число предопределенных переменных первого уравнения.

Введем обозначения:

- вектор наблюдений эндогенной переменной, для которой выполняется условие нормализации

- матрица наблюдений остальных эндогенных переменных, включенных в первое уравнение

- матрица наблюдений предопределенных переменных, включенных в первое уравнение

- матрица наблюдений предопределенных переменных, включенных в систему

-струк-ые параметры ур-ия

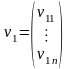- вектор случайных возмущений первого уравнения, n – объем выборки, k – число предопределенных переменных в системе.

Перепишем уравнение (10.31) в новых обозначениях:

(10.32)

Спецификацию (10.32) можно представить в стандартном виде спецификации множественной регрессионной модели:

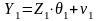, (10.33) где 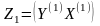- блочная матрица, - блочный столбец.

Так как элементы матрицы 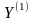коррелированы с элементами вектора , непосредственное применение МНК к структурной модели приведет к смещенным и несостоятельным оценкам. Поэтому в ДМНК поступают следующим образом:

Первый шаг:

1. Проводится регрессия каждого столбца матрицы спецификации (10.32) на все предопределенные переменные модели, т.е. рассматривается регрессия

, j=1,...,q-1, где - вектор столбец приведенных параметров k x 1 (j-я строка матрицы коэффициентов приведенной формы).

МНК-оценки вектора определяются по формуле:

.

2. По оцененной модели вычисляется оценка:

, j=1,...,q-1, и формируется матрица оценок .

Второй шаг

Строятся МНК-оценки структурных параметров и в регрессии:

(10.36)

Запишем (10.36) по аналогии с (10.33):

, (10.37) где . (10.38)

МНК-оценка параметров регрессионной модели (10.37) имеет вид:

, или

. (10.39)

На основании (10.38) вектор оценок параметров спецификации (10.37) можно представить следующим образом:

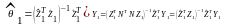, (10.40)

с учетом свойства идемпотентности матрицы N. Формула (10.40) совпадает с выражением для оценки параметров (4.22) методом инструментальных переменных. В качестве инструмента для стохастических регрессоров Z здесь используются их оценки .

Автоковариационная матрица оценок структурных параметров первого уровня определяется выражением: ,

Где 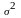- дисперсия возмущения первого уровня.

Если для уравнения выполнено ранговое условие идентификации и порядковое условие со знаком равенства (точная идентификация), то оценка ДМНК совпадает с оценкой КМНК. В большинстве экономических компьютерных пакетов для оценки одновременных уравнений реализован двухшаговый МНК.

13. Докажите, что F _{y, ŷ} = t²

R^2 – мера качества объяснения регрессионным уравнением закономерности. H₀ заключается в том, что модель не имеет объяснительной силы.

Для оценки качества R^2 можно использовать F-статистику (распределение Фишера). k – число степеней свободы (количество объясняющих переменных и свободный коэффициент), n - число экспериментов.

F монотонная функция R^2. С увеличением R^2, F увеличивается.

14. Докажите, что r_{y, ŷ} =√R²

Величина линейного коэф-та корреляции оценивает тесноту связи рассматриваемых признаков и его линейной формы, поэтому близость его к 0 еще не означает отсутствие связи м/у признаками. Корреляционное отношение. При отклонении исследуемой зависимости от линейного вида rxy=cov(x;y)/(σxσy) коэф-т корреляции r теряет свой смысл. Для оценки нелинейной корреляц-ой зависимости используют другой измеритель кор отношений. Наиболее привлекательной явл ситуация в которой хар-р выборочных данных доп-ет их группировку по оси объясняющей переменной и построение средних ординат внутри каждой группы. В этом случае в вычислении общей дисперсии заменяются вычислением дисперсии отдельных групп r2общ=σ^2внутригрупп+σ^2межгрупп.

Корр-ное отношение – есть коренное отношение групп к общей дисперсии: η=√(σ2межгрупп)/(σ2общ)

Свойства коррел отнош-я:

1. η принимает значение от 0 до 1.

2. если η=0, то связь отсутствует.

3. если η=1, то связь функциональная.

4.η≥|r|

5. если η=|r|, то имеет место точная линейная зависимость.

Коэффициентом детерминации наз-ся отношение факторной суммы квадратов отклонения к общей сумме квадратов отклонения. R2=Sфакт/Sобщ. Коэффициент хар-ет долю дисперсии результативного признака объясняемую регрессией в общей дисперсии результат приз-ка. Чем ближе R^2 к 1 тем качественнее регрессионная модель.