7. Алгоритм теста Голдфелда-Квандта на наличие (отсутствие) гетероскедастичности случайных возмущений.

_{Условие теоремы Гаусса-Маркова Ϭ(ui)=Ϭu}

Алгоритм теста:

1. сформировать служебную переменную p_i=|x_1i|+|x_2i|+…+|x_ki|

2. упорядочить уравнения наблюдений в порядке возрастания переменной p_i

3. разбить полученные уравнения примерно на 3 равные части

4. оценить модели по первой и последней частям уравнений наблюдений и вычислить для них ESS (дисперсии)

5. вычислить статистики GQ=ESS1/ESS2 и GQ^-1

6. найти значение Fкрит (через функцию FРАСПОБР)

7. сравнить полученные статистики с Fкрит. Если GQ<= Fкрит и GQ^-1<=Fкрит, то остаток в модели гомо-чен.

8. Выбор типа математической функции при построении уравнения регрессии

1.линейная у=а+bх (в-коэф.регрессии, а,х-параметры) в больше 0-прямая связь, в меньше 0 – обратная связь. Использ когда с изменением фактора, ср.значение результативн признака измен-ся равномерно. Только здесь пар-р b-абсолютный показатель силы связи. Он оценивает на сколько в среднем измен-ся результат у при изменении фактора х на 1 ед-цу.

2.парабола у=a+bх+cх² когда имеется изменение направления связи, есть мин/макс.

3.гипербола у=а+b/х если есть какое-то ограничение

4.показ-ая у=a*b^х при изучении темпов роста

5.степенная у=а*х^b

6.экспоненциальн у=е^а+bх

Для выбора математической функции проводится анализ исследуем переменных, графическое представление данных и расчет показателей аппроксимации (оценивает соотв-вие между фактич и теоретич значен результативн признака). Для графического представления используют поле корреляции, т.е. облако точек с координатами х,у

9. Выведите формулы вычисления параметров модели парной регрессии

y i ^ =а+bх i (2.18)

ei= y i- y i ^= y_i-a-bх_i. (2 .21)

Рассмотрим случай, когда имеется п наблюдений двух переменных х и у.

Предположив, что у зависит от х, мы хотим подобрать уравнение У^ = а + Ьх (2.22)

Расчетное значение зависимой переменной y i ^ и остаток ei для наблюдения i заданы уравнениями (2.18) и (2.21). Мы хотим выбрать а и Ь, чтобы минимизировать величину S:

S = = e1 + ... + en (2.23)

Можно обнаружить, что величина S минимальна, когда

b= Соv(х,у)/Var(x) (2.24) и а = . (2.25)

Варианты выражения для b

Так как

Cov(x, у) = ; (2.26) и

Var(x) = (2.27)

мы можем получить следующие выражения для Ь:

b=Cov(x,y)/Var(x)=[ ]/[ ] =[ ]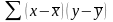/[ ] (2.28)

b=[ ]/[ ]=[ ]/[ ]

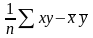10. Гетероскедастичность - понятие, проявление и меры устранения

Гетеро-ть (неоднородность) - понятие математической статистики и эконометрии; означает ситуацию, когда дисперсия ошибки в уравнении регрессии изменяется от наблюдения к наблюдению.

Меры устранения: использовать взвешенный метод наименьших квадратов; переопределить переменные; вычисление стандартных ошибок с поправкой на гетеро-ть (метод Уайта).

Проявление: означает ситуацию, когда дисперсия ошибки в уравнении регрессии изменяется от наблюдения к наблюдению. Очень часто проявление проблемы гетеро-ти можно предвидеть заранее, основываясь на знании характера статистических данных. В таких случаях можно предпринять соответствующие действия по устранению этого эффекта еще на этапе спецификации модели, т.е. на этапе формулировки вида модели.