Оценка параметров множественной регрессионной модели методом наименьших квадратов.
Множественная регрессия позволяет построить и проверить модель линейной связи между зависимой (эндогенной) и несколькими независимыми (экзогенными) переменными: y = f(x1,...,xр ), где у - зависимая переменная (результативный признак); х1,...,хр - независимые переменные (факторы).
Линейное уравнение множественной корреляции: y=a+b1x1+b2x2+…+bpxp+ε
Для оценки параметров уравнения множественной регрессии применяют метод наименьших квадратов (МНК). Для линейных уравнений и нелинейных уравнений, приводимых к линейным, строится следующая система нормальных уравнений, решение кото¬рой позволяет получить оценки параметров регрессии:
Для ее решения может быть применён метод определителей: a=∆a / ∆, b1=∆b1 / ∆,…, bp=∆bp / ∆, - определитель системы
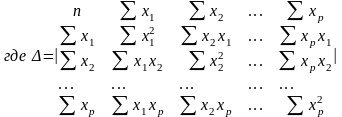
∆a, ∆b1,…, ∆bp – частные определители; которые получаются путем замены соответствующего столбца матрицы определителя системы данными левой части системы.
Оценка параметров парной регрессионной модели методом наименьших квадратов.
Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК).
МНК
позволяет получить такие оценки
параметров a и b, при которых сумма
квадратов отклонений фактических
значений результативного признака y от
расчетных (теоретических) 
минимальна:
Для того чтобы найти минимум функции, надо вычислить частные производные по каждому из параметров a и b и приравнять их к нулю. Тогда мы получаем следующую систему нормальных уравнений для оценки параметров a и b
Решая систему нормальных уравнений либо методом последовательного исключения переменных, либо методом определителей, найдем искомые оценки параметров a и b. Можно воспользоваться следующими формулами для a и b:
Эта формула получена из первого уравнения системы, если все его члены разделить на n:
где cov(x,y) — ковариация признаков; σх2— дисперсия признака х
Поскольку , получим следующую формулу расчета оценки параметра b
Таким образом явный вид решения системы нормальных уравнений:
Статистические свойства оценок
Свойство несмещенности состоит в том, что математическое ожидание оценки должно быть равно истинному значению параметра.
Свойство состоятельности состоит в том, что с увеличением наблюдений дисперсия оценки параметра стремится к нулю, т.е. оценка становится более надежной в вероятностном смысле (значения оценки более плотно концентрируются около истинного значения).
Оценка называется эффективной, если она имеет минимальную дисперсию по сравнению с любыми другими оценками этого параметра в классе выбранных процедур.
Оценка параметров эконометрической модели
Оценкой ân параметра a называют всякую функцию результатов наблюдений над случайной величиной X, с помощью которой судят о значениях параметра a.
В отличие от параметра, его оценка ã n — величина случайная. «Наилучшая оценка» ã n должна обладать наименьшим рассеянием относительно оцениваемого параметра a, например, наименьшей величиной математического ожидания квадрата отклонения оценки от оцениваемого параметра М(ã - a)2.
Оценка â n параметра a называется несмещенной, если ее математическое ожидание равно оцениваемому параметру, т. е. М(ã) = a.
В противном случае оценка называется смещенной.
Если это равенство не выполняется, то оценка ã, полученная по разным выборкам, будет в среднем либо завышать значение a (если М(ã) > a, либо занижать его (если М(ã) < 0). Таким образом, требование несмещенности гарантирует отсутствие систематических ошибок при оценивании.
Оценка â n параметра a называется состоятельной, если она удовлетворяет закону больших чисел, т.е. сходится по вероятности к оцениваемому параметру:
В случае использования состоятельных оценок оправдывается увеличение объема выборки, так как при этом становятся маловероятными значительные ошибки при оценивании. Поэтому практический смысл имеют только состоятельные оценки.
Несмещенная оценка ã n параметра a называется эффективной, если она имеет наименьшую дисперсию среди всех возможных несмещенных оценок параметра a, вычисленных по выборкам одного и того же объема n.
Так как для несмещенной оценки M(ã n - a)2 есть ее дисперсия, то эффективность является решающим свойством, определяющим качество оценки.
Для нахождения оценок параметров (характеристик) генеральной совокупности используется ряд методов.
Указанные критерии оценок (несмещенность, состоятельность, эффективность) обязательно учитываются при разных способах оценивания.