1. F-тест качества спецификации множественной регрессионной модели.

F-тест - оценивание качества уравнения регрессии - состоит в проверке гипотезы Н₀ о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического F_факт и критического (табличного) F_табл значений F-критерия Фишера. F_факт определяется как

гду n — число единиц совокупности; m - число параметров при переменных х

F_табл – это максимально возможное значение критерия под влия­нием случайных факторов при данных степенях свободы и уровне значимости а. Уровень значимости а - вероятность отвергнуть пра­вильную гипотезу при условии, что она верна.

Если F_табл<F_факт, то Н₀ - гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность. Если F_табл>F_факт, то гипотеза Н₀ не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.

2. Автокорреляция случайного возмущения. Причины. Последствия.

Зависимость возмущений в различные моменты времени называется автокорреляцией (сериальной корреляцией). При наличии автокорреляции между элементами вектора случайных возмущений, его количественные характеристики равны:

Е{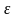 }=0

,

Где Ϭ²- дисперсия возмущения.

Причины автокорреляции

Основными причинами в регрессион. моделях являются:

1. ошибки спецификации модели ( пропуск объясняющей переменной, использование ошибочной функциональной зависимости между переменными и т.д.)

2. ошибки измерений

3. характер наблюдений (напр. данные временных рядов).

Последствия автокорреляции

При наличии автокорреляции МНК обеспечивает несмещенные оценки параметров, т. к. первая предпосылка Гаусса-Маркова выполняется,

Е{b^}=E{AY}=AXb+AE{ }=b,

Но оценка дисперсии возмущения смещенная: Е{s^2} .

Это можно показать след образом. В качестве оценки дисперсии возмущения используется оценка: .

Вектор остатков регрессии е=М при наличии автокорреляции возмущений имеет следующие основные количественные характеристики:

Е(е)=0

.

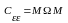В этом случае

,

Что приводит к нарушению свойства несмещенности оценки дисперсии возмущения.

Смещенность оценки дисперсии возмущений приводит к неадекватным оценкам:

1. автоковариационной матрицы оценок параметров

2) границ доверительных интервалов параметров модели и значений эндогенной переменной.

3. Автокорреляция уровней временного ряда и ее последствия.

При наличии во временном ряде тенденции и циклических колебаний значения каждого последующего уровня зависят от предыдущих. Корреляционную зависимость между последова­тельными уровнями временного ряда называют автокорреляцией уровней ряда.

Количественно ее можно измерить с помощью линейного ко­эффициента корреляции между уровнями исходного временного ряда и уровнями этого ряда, сдвинутыми на несколько шагов во времени. Коэффициент корреляции имеет вид:

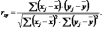
В качестве переменой x рассмотрим ряд   в качестве переменной y – ряд   Тогда коэффициент автокорреля­ции первого порядка:

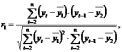
где 

Коэффициент автокорреляции первого порядка измеряет зависимость между соседними уровнями рядаt и t-1, т.е. при лаге 1.

Аналогично можно определить коэффициенты  автокорреляции второго и более высоких порядков. Так, коэффициент авто­корреляции второго порядка характеризует тесноту связи между уровнями уt и yt-2  и определяется по формуле:

 где 

Число периодов, по которым рассчитывается коэффициент автокорреляции, называют лагом. С увеличением лага число пар значений, по которым рассчитывается коэффициент автокорре­ляции, уменьшается.  Некоторые авторы считают целесообразным для обеспечения статистической достоверности коэффициентов корреляции использовать правило – максимальный лаг должен быть не больше (n/4).

Последовательность коэффициентов автокорреляции уров­ней первого, второго и т. д. порядков называют автокорреляцион­ной функцией временного ряда. График зависимости ее значений от величины лага на­зывается коррелограммой.

Анализ автокорреляционной функции и коррелограммы позволяет определить лаг, при котором автокорреляция наиболее высокая, а следовательно, и лаг, при котором связь между текущим и предыдущими уровнями ряда наиболее тесная, т.е. при помощи анализа автокорреляционной функции и коррелограммы можно выявить структуру ряда.

Последствия автокорреляции: 1. Истинная автокорреляция не приводит к смещению оценок коэффициентов регрессии. 2. Положительная автокорреляция (наиболее важный для экономики случай) приводит к увеличению дисперсии оценки коэффициентов. (более сложные случаи, в том числе лаговые переменные, рассматриваются далее). 3. Автокорреляция вызывает занижение оценок стандартных ошибок коэффициентов.