Экстремум функции нескольких переменных. Необходимое и достаточное условие экстремума.
Экстре́мум (лат. extremum — крайний) в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум).
Определения.
Пусть
дана функция
и
— внутренняя точка области
определения
Тогда
называется точкой локального максимума функции , если существует проколотая окрестность
такая, что
называется точкой локального минимума функции
если существует проколотая окрестность
такая, что
Если неравенства выше строгие, то называется точкой строгого локального максимума или минимума соответственно.
называется точкой абсолютного (глобального) максимума, если
называется точкой абсолютного минимума, если
Значение
функции
называют (строгим) (локальным) максимумом
или минимумом в зависимости от ситуации.
Точки, являющиеся точками (локального)
максимума или минимума, называются
точками (локального) экстремума.
Необходимое условие экстремума
Теорема (Необходимое условие экстремума) - если функция нескольких переменных
u
= f(
,
,
… ,
)
имеет экстремум в некоторой точке, то
в этой точке каждая ее частная производная
равна нулю или не существует.
Следствие
1.
Пусть функция нескольких переменных
имеет в точке
экстремум. Тогда:
если в точке а определен градиент функции
то он равен нулю:
если функция дифференцируема в точке а, то
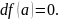
Два условия:
Функция одного переменного. Пусть
– точка экстремума (максимума или
минимума) функции у
= f(x).
Тогда в этой точке производная
равна нулю или не существует.Функция многих переменных. Пусть
равны нулю (i
= 1, 2, …, n),
либо хотя бы одна из них не существует.
Достаточное условие экстремума
Пусть функция дифференцируема в некоторой окрестности точки , кроме, быть может, самой этой точки, и непрерывна в точке . Если производная функции меняет знак с минуса на плюс при переходе через эту точку слева направо, то – точка минимума. Если производная функции меняет знак с плюса на минус при переходе через эту точку слева направо, то – точка максимума.
Пусть
– стационарная точка функции f (x), и
существует
.
Если
то
– точка минимума; если
то
– точка максимума функции f (x).
Так,
производная функции f (x) = |x| равна –1 при
отрицательных x и +1 при положительных
x. Функция |x| достигает в точке своего
минимума.
В точке = 0 первая производная функции f (x) = – равна f ′ (x0) = –2 = 0, а вторая производная f ′′ ( ) = (–2x)′ = –2 < 0. Функция – + 3 достигает в точке = 0 своего максимума.
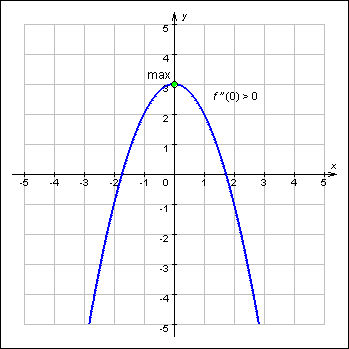
График 3.2.2.2.Достаточные условия экстремума. График 3.2.2.3.Достаточные условия экстремума.
Заметим,
что в точке x = 0 функции y =
вторая производная f ′′ (
)
= 0, однако эта точка является точкой
минимума. Можно доказать, что если f ′
(x0) = f ′′ (
)
=... = f (2n – 1) (
)
= 0 и f (2n) (
)
> 0 (f (2n) (
)
< 0), то точка
является точкой минимума (соответственно,
максимума).