Градиент скалярной функции.
u
= f (x, у, z),
заданной в некоторой области пространства
(X
Y Z),
есть вектор с проекциями
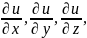обозначаемый символами: grad
,
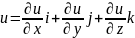где i,
j,
k
— координатные орты. График
функции
— есть функция точки (х,
у, z),
т. е. он образует векторное поле.
Производная в направлении графика
функции в данной точке достигает
наибольшего значения и равна:
Направление градиента есть направление наибыстрейшего возрастания функции. График функции в данной точке перпендикулярен поверхности уровня, проходящей через эту точку.
Касательная плоскость и нормаль к поверхности.
Определение
1.
Касательной
плоскостью к поверхности в данной точке
P
(
)
называется плоскость, проходящая через
точку Р
и содержащая в себе все касательные,
построенные в точке Р
ко всевозможным кривым на этой поверхности,
проходящим через точку Р.
Пусть поверхность s задана уравнением F (х, у, z) = 0 и точка P ( ) принадлежит этой поверхности. Выберем на поверхности какую-либо кривую L, проходящую через точку Р.
Пусть х = х(t), у = у(t), z = z(t) – параметрические уравнения линии L.
Предположим, что:
1) функция F(х, у, z) дифференцируема в точке Р и не все её частные производные в этой точке равны нулю;
2) функции х(t), у(t), z(t) также дифференцируемы.
Поскольку кривая принадлежит поверхности s , то координаты любой точки этой кривой, будучи подставленными в уравнение поверхности, обратят его в тождество. Таким образом, справедливо тождественное равенство: F [x(t), у(t), z (t)] = 0.
Продифференцировав это тождество по переменной t, используя цепное правило, получим новое тождественное равенство, справедливое во всех точках кривой, в том числе и
в точке P ( ):
Пусть
точке Р
соответствует значение параметра
,
то есть
= x
(
),
= y
(
),
= z
(
).
Тогда
последнее соотношение, вычисленное в
точке Р,
примет вид
Формула представляет собой скалярное произведение двух векторов. Первый из них – постоянный вектор
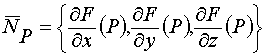
не
зависящий от выбора кривой на поверхности
.
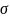Второй
вектор
– касательный в точке Р
к линии L,
а значит, зависящий от выбора линии на
поверхности, то есть является переменным
вектором.
П
ри
введённых обозначениях равенство
перепишем как
.
Его смысл таков: скалярное произведение
равно нулю, следовательно, векторы
и
перпендикулярны. Выбирая всевозможные
кривые (см. рис. 54), проходящие через
точку Р
на поверхности s
, мы будем иметь различные касательные
векторы, построенные в точке Р
к этим линиям; вектор же
от этого выбора не зависит и будет
перпендикулярен любому из них, то есть
все касательные векторы
расположены в одной плоскости, которая, по определению, является касательной к
поверхности s, а точка Р в этом случае называется точкой касания. Вектор является направляющим вектором нормали к поверхности.
Определение 2. Нормалью к поверхности s в точке Р называется прямая, проходящая через точку Р и перпендикулярная к касательной плоскости, построенной в этой точке.
Мы доказали существование касательной плоскости, а, следовательно, и нормали к поверхности. Запишем их уравнения:
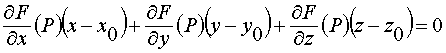(18)
(18) – уравнение касательной плоскости, построенной в точке P ( ) к поверхности s , заданной уравнением F(х, у, z) = 0;
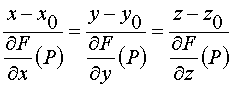(19)
(19) – уравнение нормали, построенной в точке Р к поверхности s .