Ряд Фурье 2п-периодических функций. Теорема Дирихле. Разложение в ряд Фурье периодических функций с произвольным периодом, непериодических функций, четных, нечетных функций.
Частные производные. Дифференцируемость. Полный дифференциал.
Частные
производные. В предыдущих примерах мы
использовали производные от f
(x,y)
по х и по у. Рассмотрим теперь такие
производные в более общем плане. Если
у нас имеется функция двух переменных,
например, F(x,y)
=
– xy,
то мы можем определить в каждой точке
две ее «частные производные», одну –
дифференцируя функцию по х и фиксируя
у, другую – дифференцируя по у и фиксируя
х. Первая из этих производных обозначается
как fўx(x,y)
или f/x;
вторая – как fўy(x,y)
или f/y.
Если f(x,y)
=
– xy,
то f/x
= 2x
– y
и f/y
= –x.
Заметим, что частные производные от
любой функции – это, вообще говоря,
новые функции. На практике эти функции
в свою очередь дифференцируемы. Частные
производные от fўx
по х и у принято обозначать, соответственно,
и или 2f/x2
и 2f/xy;
аналогичные обозначения используются
и для частных производных от fўy.
Если обе смешанные производные (по х и
у, по у и х) непрерывны, то 2f/xy
= 2f/yx;
в нашем примере 2f/xy
= 2f/yx
= –1.
Частная производная fўx(x,y) указывает скорость изменения функции f в точке (x,y) в направлении возрастания х, а fўy(x,y) – скорость изменения функции f в направлении
возрастания
у. Скорость изменения функции f
в точке (х,у) в направлении прямой,
составляющей угол q
с положительным направлением оси х,
называется производной от функции f
по направлению; ее величина представляет
собой комбинацию двух частных производных
от функции f
– по х и по у, и равна
Дифференци́руемая фу́нкция в математическом анализе — это функция, которая может быть хорошо приближена линейной функцией. Дифференцируемость является одним из фундаментальных понятий в математике и имеет большое число приложений как внутри неё, так и в естественных науках, широко использующих математический аппарат.
Определение.
Пусть дана функция
,
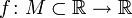и
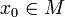— внутренняя точка области определения
f.
Тогда f
называется дифференци́руемой
в
,
если существует окрестность
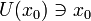и число
такие,
что в этой окрестности для f
справедливо представление
где
o(x
−
)
обозначает величину, пренебрежимо малую
по сравнению с x
−
при
Если f
дифференцируема в
,
пишут
Линейное отображение
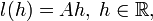где A — константа из предыдущего
определения, называется дифференциа́лом
функции f в точке
и обозначается df(
).Функция z = f(x;y) называется дифференцируемой в точке M(x;y), если ее полное приращение в этой точке можно представить в виде Δz = AΔx + BΔy + αΔx + βΔy,
где,
и
при
,
Свойства:
Функция дифференцируема в точке тогда и только тогда, когда у неё существует конечная производная. Более того
Дифференциал функции (соответственно производная) определяется единственным образом.
Функция, дифференцируемая в какой-либо точке, непрерывна в ней же, то есть
Обратное, вообще говоря, неверно.
Полный дифференциал
Функции f (x, у, z,...) нескольких независимых переменных — выражение
в случае, когда оно отличается от полного приращения (См. Полное приращение)
Δf = f (x + Δx, y + Δy, z + Δz,…) - f (x, y, z, …)
на величину, бесконечно малую по сравнению с
