2. Знакопеременные и знакочередующиеся ряды. Абсолютная сходимость. Признак Лейбница, Схема исследования знакочередующегося ряда.

Знакоположительные числовые ряды.

Теорема 1: Критерий сходимости знакоположительных рядов.

Ряд сходится последовательность частичных сумм ограничена.

Теорема 2: Первый признак сравнения.

Пусть . Тогда:

1. Если сходится, то сходится.

2. Если расходится, то расходится.

Теорема 3: Второй признак сравнения.

Пусть и - знакоположительные ряды, причём при . Тогда эти два ряда сходятся или расходятся одновременно.

Определение 1. Ряд называется знакочередующимся, если он имеет вид:

(или ), где

Ряды, не являющиеся знакопостоянными ( или ) называются знакопеременными.

Например, 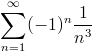- знакочередующийся ряд, - знакопеременный ряд.

Признак Даламбера и оба признака Коши в случае знакопеременных и знакочередующихся рядов не работают!

Определение 2. Ряд называется абсолютно сходящимся, если сходится.

Определение 3. Ряд называется условно сходящимся, если он сходится, но не является абсолютно сходящимся.

Теорема 4: Абсолютно сходящийся ряд сходится.

Теорема 5: Признак Лейбница.

Пусть монотонно невозрастает и . Тогда ряд сходится.

Схема исследования знакочередующегося ряда

Вид ряда, его тип	Схема исследования
ФОРМУЛЫ	1! 2! обобщенный гармонический ряд геометрическая прогрессия
II. Числовой знакочередующийся ряд , - действительные числа, .	II.1. Применим необходимый признак: Если ряд сходится, то , при . Если , то ряд расходится. Если , то переходим к следующему пункту. II.2. Применим признак Лейбница сходимости знакочередующихся рядов: Если и , то ряд сходится. II.3. Исследуем ряд на абсолютную сходимость: Ряд сходится абсолютно, если сходится ряд . Ряд сходится условно, если он сходится, а ряд расходится. Для сходимости знакоположительного ряда применяем пункт I.2.

3. Степенной ряд, теорема Абеля, Интервал и радиус сходимости степенного ряда.

Определение 1.

Ряд, членами которого являются степенные функции аргумента x, называется степенным рядом:

Часто рассматривается также ряд, расположенный по степеням (x − ), то есть ряд вида

где − действительное число.

Теорема 1.1. (теорема Абеля). Если степенной ряд сходится при некотором , где -число, не равное нулю, то он сходится абсолютно при всех значениях x таких, что . Наоборот, если ряд расходится при , то он расходится при всех значениях x таких, что .

Доказательство. Пусть числовой ряд

(1.3)

сходится. Поэтому Но любая последовательность, имеющая предел, ограничена, значит, существует такое число M, что для всех n=0,1,2,…

Рассмотрим теперь ряд

(1.4)

предполагая, что Так как и при этом то члены ряда (3.4) не превосходят соответствующих членов сходящегося ряда

(геометрической прогрессии). Следовательно, ряд (1.4) сходится, а ряд (1.2) абсолютно сходится.

Предположим теперь, что ряд (1.3) расходится, а ряд (1.2) сходится при Но тогда из сходимости ряда (1.2) следует сходимость и ряда (1.3), что противоречит предположению. Теорема доказана.

Интервал и радиус сходимости степенного ряда.

Так называется интервал, в каждой точке которого степенной ряд с действительными членами сходится, причем абсолютно. На каждом из концов этого интервала ряд может как сходиться (абсолютно или условно), так и расходиться. Вне этого интервала ряд расходится. Заметим, что интервал сходимости существует для каждого сходящегося хоть на каком-нибудь интервале степенного ряда. Для ряда, сходящегося только в одной точке, интервал получается вырожденным. Для расходящегося ряда интервал равен пустому множеству.

Для степенного ряда радиус R (половина длины) интервала сходимости можно вычислить по формуле Коши-Адамара:

причем считают, что если этот верхний предел равен нулю, то ряд сходится на всей числовой оси (радиус сходимости бесконечен), а если предел равен бесконечности, то радиус сходимости равен нулю.

Верхний предел числовой последовательности { } – наибольший из пределов частичных подпоследовательностей, которые можно составить из членов данной последовательности. Он обозначается как