34. Статистическая гипотеза. Статистический критерий. Алгоритм проверки статистических гипотез.

Статистические гипотезы. Определение.

Пусть в (статистическом) эксперименте доступна наблюдению случайная величина X, распределение которой P известно полностью или частично. Тогда любое утверждение, касающееся P называется статистической гипотезой. Гипотезы различают по виду предположений, содержащихся в них:

• Статистическая гипотеза, однозначно определяющая распределение P, то есть H : {P= }, где какой-то конкретный закон, называется простой.

• Статистическая гипотеза, утверждающая принадлежность распределения к некоторому семейству распределений, то есть вида 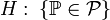, где P — семейство распределений, называется сложной.

Статистический критерий — строгое математическое правило, по которому принимается или отвергается та или иная статистическая гипотеза с известным уровнем значимости. Построение критерия представляет собой выбор подходящей функции от результатов наблюдений (ряда эмпирически полученных значений признака), которая служит для выявления меры расхождения между эмпирическими значениями и гипотетическими.

Определение.

Пусть даны выборка из неизвестного совместного распределения , и семейство статистических гипотез , …. Тогда статистическим критерием называется функция, устанавливающая соответствие между наблюдаемыми величинами и возможными гипотезами:

Таким образом каждой реализации выборки статистический критерий сопоставляет наиболее подходящую с точки зрения этого критерия гипотезу о распределении, породившем данную реализацию.

Алгоритм проверки статистических гипотез.

• Выдвигают нулевую гипотезу о нормальном законе распределения случайной величины X и находят его параметры xв и S.

• Определяют теоретические частоты ni’, соответствующие опытным частотам. Если среди опытных частот имеются малочисленные, то их необходимо объединить с соседними. Интервалы после объединения будем обозначать (ai;bi]. Число интервалов должно быть не менее 4-х. Если случайная величина X непрерывна, то

• По формуле вычисляют величину.

• Определяем число степеней свободы k= l-3, где l – число интервалов после объединения.

• Находят уровень значимости a=1-g, где g – доверительная вероятность; при g=0,95 , g=0,05.

• По таблице при заданных a и k находят значение, которое является критической точкой.

• Если , нет оснований отвергнуть нулевую гипотезу.

Если , нулевую гипотезу отвергают.

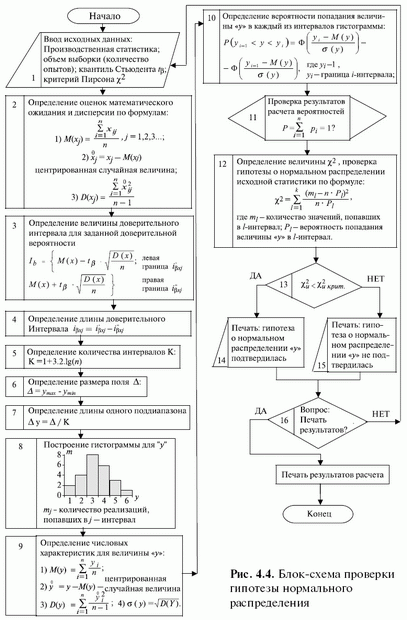
35. Схема проверки гипотезы о нормальном законе распределения генеральной совокупности по критерию Х-квадрат.