Классическое определение вероятности события. Теоремы сложения, умножения.
ОПРЕДЕЛЕНИЕ (классическое определение вероятности). Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу.
Итак, вероятность события А определяется формулой:
где m – число элементарных исходов, благоприятствующих А; n – число всех возможных элементарных исходов испытания.
Свойства:
Вероятность достоверного события равна единице.
Действительно, если событие достоверно, то каждый элементарный исход испытания благоприятствует событию. В этом случае m=n, следовательно, P(A)=m/n=n/n=1 .
Вероятность невозможного события равна нулю.
В этом случае m=0, следовательно, P(A)=m/n=0/n=0
Вероятность случайного события есть положительное число, заключенное между нулем и единицей.
Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных исходов испытания. В этом случае 0<m<n, значит 0<m/n<1, следовательно,
0<P(A)<1
Итак, вероятность любого события удовлетворяет двойному неравенству
0<P(A)<1
Теоремы сложения, умножения.
ОПРЕДЕЛЕНИЕ. Суммой А+В двух событий А и В называют событие, состоящее в появлении события А, или события В, или обоих этих событий.
Теорема 1.(теорема сложения вероятностей)
Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
P(A+B)=P(A)+P(B) (3)
Доказательство:
Введем обозначения: n
– общее число возможных элементарных
исходов испытания;
– число исходов, благоприятствующих
событию А;
– число исходов, благоприятствующих
событию В.Число
элементарных исходов, благоприятствующих
наступлению либо события А,
либо события В,
равно
+
.
Следовательно, P(A+B)=(
+
)/n=
.
Приняв во внимание, что
/n=P(A)
и
/n=P(B),
окончательно получим P(A+B)=P(A)+P(B).
Следствие 1. Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
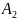P(
+
+...+
)=P(
)+P(
)+...+P(
)
Теорема 2. (теорема умножения вероятностей)
Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:
Следствие
2.
Эту теорему можно обобщить на любое
конечное число зависимых событий
,
,...,
P(
,
,...,
)=P(
)•
(
)•
(
)...
(A)
Событие
В
называют независимым от события А,
если появление события А
не изменяет вероятности события В,
т.е. если условная вероятность события
В
равна его безусловной вероятности
B=P(B).
Формулы полной вероятности, формула Байеса переоценки гипотез.
Формула полной вероятности.
Пусть
событие A
может произойти только вместе с одним
из попарно несовместных событий
,
образующих полную группу. Тогда, если
произошло событие A,
то это значит, что произошло одно из
попарно несовместных событий,
A,
A,
...,
.
Следовательно,
Применяя аксиому сложения вероятностей, имеем
Но
(i=1, 2, ..., n), поэтому
Эта формула называется формулой полной вероятности. События часто называют «гипотезами».
формула Байеса переоценки гипотез
Формула, имеющая вид:
где
,
,...,
— несовместимые события,
Общая схема применения формулы вероятности
гипотез: если событие В
может происходить в различных условиях,
относительно которых сделано n
гипотез
,
,
...,
с известными до опыта вероятностями
P(
),
P(
),
..., Р(
)
и известны условные вероятности
P(B/
),
то после опыта, где наступило событие
В.
Происходит переоценка вероятностей
гипотез (в силу чего эту формулу называют
формулой вероятности гипотез). Формула
Байеса
может быть использована для оценки
перспективности территорий, оценки
палеогеографических реконструкций,
направления разведки и т. п.