22. Построение поверхностного интеграла I и II рода. Поверхностный интеграл к двойному.

Не писал, так как все в лекции должно быть и там просто ппц, по другому.

23. Векторное и скалярное поле. Градиент. Дивергенция поля. Циркуляция векторного поля. Формула Стокса.

Определение 1: Если в каждой точке M(x,y,z) некоторой области V пространства (или плоскости) определена скалярная функция u = u(M), то говорят, что в области V задано скалярное поле u = u(M) = u(x,y,z).

Примерами скалярных полей являются: поле температуры T внутри тела, поле потенциала электрического заряда, поле плотности тела и т.д.

Определение 2: Если в каждой точке M(x,y,z) некоторой области V пространства (или плоскости) определен вектор

то говорят , что в области V задано векторное поле

Примерами векторных полей являются: поле скоростей текущей жидкости, поле электрической напряженности , поле магнитной напряженности и т.д.

Важнейшими характеристиками скалярных и векторных полей являются градиент (grad) скалярного поля, дивергенция(div) и ротор(rot) векторного поля.

Определение 3: Градиентом дифференцируемого скалярного поля u(M)=u(x,y,z) называется вектор

Т.е. сумма частных производных умноженных на соответствующие единичные вектора.

Определение 4: Дивергенцией (или расходимостью) дифференцируемого векторного поля называется скаляр

Определение 5: Ротором (или вихрем) дифференцируемого векторного поля называется вектор

который с помощью символической записи удобно представить в виде векторного произведения

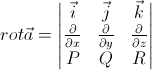
Операторы grad, div,rot называются основными операторами теории поля.

В качестве примеров использования операторов градиента скалярного поля, дивергенции и ротора векторного поля приведем формулу связи напряженности и потенциала электростатического поля: и систему уравнений Максвелла для стационарного электромагнитного поля:

1)

2)

3)

4)

Теорема Стокса — одна из основных теорем дифференциальной геометрии и математического анализа об интегрировании дифференциальных форм, которая обобщает несколько теорем анализа.

Пусть — кусочно-гладкая поверхность (p=2) в трёхмерном евклидовом пространстве (n=3), F — дифференцируемое векторное поле. Тогда циркуляция векторного поля вдоль замкнутого контура равна потоку ротора (вихря) поля через поверхность , ограниченную контуром:

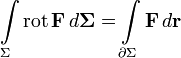
или в координатной записи:

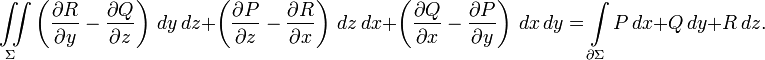
24. Поток через замкнутую поверхность Формула Остроградского-Гаусса.

Формула Остроградского

Пусть теперь — кусочно-гладкая гиперповерхность ( ), ограничивающая некоторую область в -мерном пространстве. Тогда интеграл дивергенции поля по области равен потоку поля через границу области :

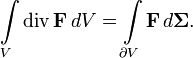
Что эквивалентно записи:

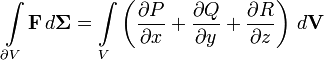
или

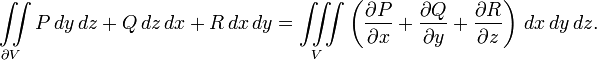
Вывод из теоремы Стокса

Рассмотрим дифференциальную форму .

Тогда, используя свойство дифференциала дифференциальной формы :

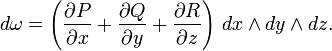
Отсюда, используя теорему Стокса:

25. Элементы комбинаторики.

Комбинато́рика (Комбинаторный анализ) — раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисления элементов) и отношения на них (например, частичного порядка). Комбинаторика связана со многими другими областями математики — алгеброй, геометрией, теорией вероятностей и имеет широкий спектр применения в различных областях знаний (например в генетике, информатике, статистической физике).

Термин «комбинаторика» был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве».

Иногда под комбинаторикой понимают более обширный раздел дискретной математики, включающий, в частности, теорию графов.

• Структурная комбинаторика - данный раздел, относящийся к некоторым вопросам теории графов, а также теории матроидов.

• Перечислительная комбинаторика (или исчисляющая комбинаторика) рассматривает задачи о перечислении или подсчёте количества различных конфигураций (например, перестановок) образуемых элементами конечных множеств, на которые могут накладываться определённые ограничения, такие как: различимость или неразличимость элементов, возможность повторения одинаковых элементов и т. п.

• Теория Рамсея изучает наличие регулярных структур в случайных конфигурациях элементов. Примером утверждения из теории Рамсея может служить следующее:

в группе из 6 человек всегда можно найти трёх человек, которые либо попарно знакомы друг с другом, либо попарно незнакомы.

• Вероятностная комбинаторика - какова вероятность присутствия определённого свойства у заданного множества.

• Топологическая комбинаторика (англ.) применяет идеи и методы комбинаторики в топологии, при изучении дерева принятия решений, частично упорядоченных множеств, раскрасок графа и др.

• Инфинитарная комбинаторика (англ.) — применение идей и методов комбинаторики к бесконечным (в том числе, несчётным) множествам.