28. Геометр.Смысл модуля и аргумента производной фкп. Конформные отобр-я.

Пусть дана анал-ая ф. оперед-на в нек. открытом множестве D. Причем f’(z)≠0. Выберем любую т.z₀ D и рас-им или . Образом круга |∆z|< на множестве W яв-ся множество точек соответ-х приращению ∆z. Т.к.f(z) – диф-ая ф-я, то ∆f(z) : f’(z₀)∆z+ с точностью до б.м.высшего порядка.

Запишем в показ-ой форме: ; ; ; 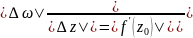⇒модуль есть коэф-нт растяжения при отображении ф-и f(z) одинаковой во всех направ-ях.

т.е. аргумент производной есть угол поворота при отображении ф-и f(z) одинаковой для всех точек окрестности. Т.о., чтобы найти образ круга при отображении анал-ой ф-и f(z), надо все точки круга растянуть в |f’(z₀)| раз. Повернуть все точки круга на угол f’(z₀)

Определение. Отображение, сохр-ее углы между кривыми, наз-ся конформным.

Условия конформности отображения:

1.f(z) взаимно однозначная функция

2.f(z) аналитическая функция

3.f’(z)≠0

Конф-е отобр-я для нек-х ф-й отображение осущ-ся этой ф-ей конформно на всей КП за искл. т.z=0, z=∞. Любая прямая, проходящая через т.z=0 с ур-м argz=k отображается в прямую с ур-м z=nk, т.е.в т.z=0 углы не сохраняются.

29. Интеграл от фкп. Св-ва интеграла. Интеграл с переменным верхним пределом. Теорема Мореры.

Пусть f(Z)=U+iV непр-а в обл. Д и L- гладкая кривая, целиком лежащая в Д. Тогда интеграл от фкп по кривой l опред-я след.образом:∫f(Z)dZ=∫(U+iV)(dx+idy)=∫Udx-Vdy+i∫Vdx+Udy.

lZl=R, lZ-Z₀ l=R, Z=Z₀ +Re^it

Z=Re^it -параметр.ур-е окр-ти с центром в начале координат и радиусом R.

∫_lZ-Z0l=R=dZ/(Z-Z₀)=2Пi

Свойства интегралов от фкп

линейность∫(c1f1(Z)+c2f2(Z))dZ=

=c1∫f1(Z)dZ+c2∫f2(Z)dZ

при изменении ориентации дуги интеграл меняет знак ∫_L+ f(Z)dZ=-∫_L- f(Z)dZ

оценка модуля интеграла l∫f(Z)dZl<=∫lf(Z)ldZ

если М-макс.lf(Z)l , то l∫f(Z)dZl≤ML, L-длина дуги.

Интеграл с переменным верхним пределом:

Пусть L- гладкая кривая, соед-ая т. Z₀ и Z. Если ф-я f(Z) яв-ся анал-ой в обл., в которой нах.ся кривая L, то интеграл от нее не зависит от пути интегр-я, а зависит лишь от нач. и кон. точки. В этом случае интеграл принято обозначать ∫_Z0^Z f(Z)dZ=F(Z), где

F(Z)-первообразная для f(Z) _.

Теорема Мореры: Если ф-я f(Z) непр. в обл. Д и ∫f(Z)dZ не зависит от пути интег-я ( в частности, это выполняется, если f(Z) яв-ся аналитической), то F(Z) яв-ся аналитической, причем F(Z)=f(Z).

30. Интегральные теоремы Коши для односвязной и многосвязной областей.

Если ф-я f(Z) анал-а в замкнутой односвязной обл. Д с границей Г, то:

Интегральная теорема Коши для многосвязной области.

Пусть f(Z)анал-ая ф-я в многосвязной обл. Д, имеющей гладкую внешнюю границу Г и гладкие внутренние контуры γ1, γ2, …, γn. Обход всех контуров против часовой стрелки, тогда

∫по замкн.конт.f(Z)dZ=∑ ∫ по замк.конт. f(Z) dZ

31. Формула Коши для односвязной области.

Если D - односвязная ограниченная область, w = f( z) - аналитическая в этой области функция, то для любого кусочно-гладкого замкнутого контура L, лежащего в D, интеграл от f(z) по L равен нулю: 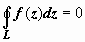. 32. Формулы Коши для производных. Бесконечная дифференцирусмость аналитических функции.

Пусть  — область на комплексной плоскости с кусочно-гладкой границей , функция  — аналитично в и  — точка внутри области . Тогда справедлива следующая формула Коши:

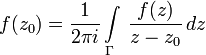
Если функция f(z) имеет в каждой точке области D производную первого порядка ( т.е. аналитична в области D), то она имеет в этой области производную любого порядка (т.е. любая производная функции f(z) аналитична в области D).