22. Связь между ду n-го порядка и системой ду n-го порядка. Метод исключения.

y⁽ⁿ⁾ = f(x, y, y’, y’’…y^(n-1)) – диф. ур-е n-го порядка. Оно может быть сведено к системе ДУ, если положить систему:

y = y₁

y’ = y₂= y₁’

y’’= y₃= y₁’’

y^(n-1) = y_n = y₁^(n-1)

y⁽ⁿ⁾ = f(x, y₁, y₂…y_n)

Реш-м системы яв-ся вектор: ,первая координата которого явл-ся реш-ем ДУ. Обратно, в нек. случаях систему ДУ можно свести к 1 ДУ. На этом основан один из методов реш-я систем ДУ, который наз-ся методом исключения.

23. Фкп. Предел, непрер-ть, св-ва ф-й, имеющих предел.

Если каждой т.z из обл. D комп. пл-ти Z по к.-л. правилу ставится в соответствие число w в обл. E, на пл-ти W, то говорят, что на множестве D задана ф-я комп-го переменного f(z)|D→E. ФКП f(z) наз-ся однозначной, если каждому числу z из обл. D ставится в соответ-е един-ое число w из обл. E. В противном случае ф-я наз-ся многозначной.

Пусть ф-я w=f(z) опр. в нек. (z₀).

Определение: Число а наз-ся пределом ф-и f(z) при z→ z₀ если:

При этом z→z₀ всевозможными путями. Ф-и, имеющие предел в т.z₀ обладают св-ми, анал-ми св-м ф-и действ-го переем-го:

_1.Если _, то он единственный.

_2.Если то найдётся в которой f(z) ограничена, т.е | f(z)|≤ M; для любых z ϵ

_3.Если = a ≠ 0, то найдётся в которой f(z) ≠ 0.

_4.Если и то

Определение: Ф-я f(z) наз-ся непр. в т.z₀ если f(z) определена в u(z₀) и ;

Ф-я f(z) непр. только тогда, когда непр. её действ. и мнимая части.

24. Показ-я, тригон-ие, гипер-ие, логар-ая, общая степенная и общая показ-ая фкп.

Показательная функция:

w = e^z = e^x+iy = e^xe^iy = e^x (cos y + i sin y)

Тригонометрические функция:

Sin z = Cos z =

Sin z = sin (x+ iy) = sin x ch y + i cos x sh y

Cos z = cos (x+ iy) = cos x ch y - i sin x sh y

Гиперболические функции:

= ; ch z =

Связь с тригонометрическими формулами:

shz = ; ch z = cos (iz)

Логарифмическая функция:

Лог-я ф-я Lnz опред-а на всей КП, кроме т. z=0

Общая степенная функция:

;

Общая показательная функция

;

25. Обратные тригонометрические и гиперболические фкп.

Обратные тригонометрические ф-и опред-ся как ф-и обратные тригонометрическим.

Все обратные тригонометрические ф-и яв-ся многозначными. Главные значения их (arcsin,…) получаются при k=0.

Обратные гиперболические ф-и.

)

26. Производная фкп. Необходимые условия дифференцируемости функции в точке

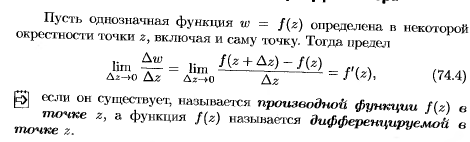
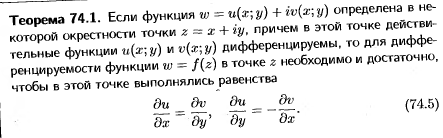
27. Дост.Усл-я диф-ти ф-и.Анал-ие и гармон-е ф-и.

ТЕОРЕМА(Дост. усл-е диф-ти ФКП):Если ф-и U(x,y) и V(x,y) имеют в т.(x₀, y₀) непр. частные производные, удовл-ие усл-ю Коши-Римана, то ф-я f(z) диф-ма в т.z₀=x₀+iy₀

Определение. Ф-я f(z) наз-ся анал-ой в т.z₀, если она диф-ма в самой т.z₀, и в нек. U(z₀). Т.z₀, в которой ф-я f(z) анал-на, наз-ся прав-ой т. f(z)

Точка, в кот. Ф-я f(z) не анал-на или не определена, наз-ся особой точкой ф-и f(z)

Гармонические ф-и: Пусть задана ф-я f(z)=U(x,y)+iV(x,y), причем U(x,y) и V(x,y) имеют непр. частные производные до 2го порядка включ-но. Пусть f(z) анал-ая ф-я, тогда для нее выпол-ся усл-я Коши-Римана: Сложим ур-я системы Введем обозначение - оператор Лапласа

Тогда последнее ур-е можно переписать в виде ур-ие Лапласа. Ф-я удовл-я ур-ю Лапласа наз-ся гарм.ф-й, то есть мы показали, что действ-я часть анал-ой ф-и яв-ся гарм-й. Из усл-й Коши-Римана ⇒ мнимая часть анал-й ф-и яв-ся гарм-ой. Обратное верно.

ТЕОРЕМА. Всякая гарм-ая ф-я явл-я действ. или мнимой частью нек. анал-ой ф-и.