19. Метод вариации для решения лнду II-го порядка (метод Лагранжа).

Непосредственное нахождение частного решения лнду, кроме случая уравнения с постоянными коэффициентами, причем со специальными свободными членами, представляет большие трудности. Поэтому для нахождения общего решения лнду обычно применяют метод вариации произвольных постоянных, который всегда дает возможность найти общее решение лнду в квадратурах, если известна фундаментальная система решений соответствующего однородного уравнения. Этот метод состоит в следующем.

Согласно вышеизложенному, общее решение линейного однородного уравнения:

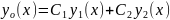, (8.1)

где – линейно независимые на некотором интервале X решения лоду, а - произвольные постоянные. Будем искать частное решение лнду в форме (8.1), считая, что – не постоянные, а некоторые, пока неизвестные, функции от : . (8.2) Продифференцируем равенство (8.2): . (8.3)

Подберем функци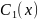и и так, чтобы выполнялось равенство: . Тогда вместо (8.3) будем иметь:

. (8.4)

Продифференцируем это выражение еще раз по . В результате получим: . (8.5) Подставим (8.2), (8.4), (8.5) в лнду 2-го порядка f(x):

f(x)

Или f(x). (8.6)

Так как - решения лоду 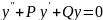, то последнее равенство (8.6) принимает вид: 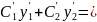f(x).

Таким образом, функция (8.2) будет решением лнду в том случае, если функции и удовлетворяют системе уравнений:

(8.7)

Так как определителем этой системы является определитель Вронского для двух линейно независимых на X решений соответствующего лоду, то он не обращается в ноль ни в одной точке интервала X. Следовательно, решая систему (8.7), найдем и : и . Интегрируя, получи , , где – произв. пост.

Возвращаясь в равенство (8.2), получим общее решение неоднородного уравнения: .

Ряды

1. Числовые ряды. Основные понятия, свойства сходящихся рядов. Необходимый признак сходимости (с док-вом).

Основные определения. Пусть дана бесконечная числовая последовательность . Числовым рядом называется составленная из членов этой последовательности запись . Или .Числа называют членами ряда; , называется общим членом ряда. В результате вычисления значений этой функции при n=1, n=2, n=3, … должны получаться члены ряда .

Пусть дан ряд (18.1.1). Составим из его членов конечные суммы, называемые частичными суммами ряда:

Определение. Если существует конечный предел S последовательности частичных сумм ряда (18.1.1) при , то говорят, что ряд сходится; число S называют суммой ряда и пишут или .

Если 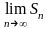не существует (в том числе бесконечен), ряд называется расходящимся.

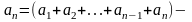
Свойства сходящихся рядов. Необходимый признак сходимости ряда. Общий член сходящегося ряда стремится к нулю при : Доказательство. Если , то и , но , следовательно .

С проверки выполнения условия надо начинать решение любой задачи на исследование сходимости ряда: если это условие не выполняется, то ряд заведомо расходится. Это условие необходимо, но не достаточно для сходимости ряда: общий член гармонического ряда (18.1.2) , однако этот ряд расходится.

Определение. Остатком ряда после n-го члена называется ряд .

Св-во 1. Если сходится ряд, то сходится любой его остаток, Обратно, если сходится какой-нибудь остаток ряда, то сходится и сам ряд.

Доказательство. Пусть - частичные суммы ряда (18.2.1); обозначим k-ую частичную сумму остатка : . Тогда 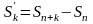. Устремим , считая n фиксированным числом. Ряд (18.2.1) сходится, т.е. существует конечный , следовательно существует конечный предел , т.е. остаток сходится. Обратное утверждение доказывается также. Так как , то из существования конечного предела следует существование конечного предела , т.е. из сходимости остатка следует сходимость ряда. Т.е. отбрасывание конечного числа начальных членов ряда или добавление в его начало нескольких новых членов не влияет на сходимость ряда.

Св-во 2. Если ряд сходится, то сумма его остатка после n-го члена стремится к нулю при .

Доказательство. Пусть S - сумма исходного ряда (18.2.1), - сумма его остатка. Из равенства следует , т.е. . Отсюда .

Из предыдущего свойства следует, что сходимость ряда определяется сходимостью его остатка, т.е. хвостом ряда, а сумма S ряда, как следует из равенства , определяется пределом , т.е. началом ряда.

Св-во 3. Если все члены сходящегося ряда умножить на одно и то же число с, то сходимость ряда сохранится, а сумма умножится на с.

Доказательство. Частичная сумма ряда есть ; по свойству предела .

Св-во 4. Два сходящихся ряда и можно почленно складывать и вычитать; ряд также сходится, и его сумма равна .

Доказательство и этого свойства - прямое следствие свойств пределов для частичных сумм: .