56, 57. Спецификация и оценивание мнк эконометрических моделей нелинейных по параметрам.
В моделях, нелинейных по параметрам, например степенных или показательных, непосредственное применение МНК для их оценки невозможно, так как необходимым условием применимости МНК является линейность по коэффициентам уравнения регрессии. В данном случае преобразованием, которое приводит уравнение регрессии к линейному виду, является логарифмирование. Логарифмические модели: Y = AXb, где А и b— параметры модели. Прологарифмируем обе части данного уравнения: ln(Y)=ln(A) + b*ln(X) = a+b*ln(X), где а= ln(A) (*). Спецификация, соответствующая (*) называется двойной логарифмической моделью: ln(Y)= a+ b*ln(X)+u, поскольку и эндогенная переменная, и регрессор используются в логарифмической форме. Введем обозначения: Y*=ln(Y), X*=ln(X)
Y*=a+b*X+u
Получаем спецификацию линейной модели, к которой при соответствующем включении случайного возмущения применим МНК.
В моделях, нелинейных по оцениваемым параметрам, но приводимых к линейному виду, МНК применяется к преобразованным уравнениям. Пусть получена МНК-оценка моделиY*=a+b*X+u:
y*=ā + bx+u
(Sā) (Sb) (Su)
Коэффициенты исходной модели и их стандартные ошибки вычисляются с учетом замены.
Нелинейный МНК. В общем случае оценка нелинейных по параметрам уравнений выполняется с помощью так называемого нелинейного метода наименьших квадратов (НМНК).
Обозначим нелинейное по параметрам уравнение регрессии f(X, ß) (X— матрица рсгрсссоров,ß — вектор параметров). Параметры уравнений в данном методе подбираются таким образом, чтобы максимально приблизить кривую f(X, ß) к результатам
наблюдений эндогенной переменной Y. Таким образом, здесь, как и в обычном
МНК, минимизируется сумма квадратов отклонений:
F=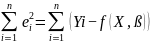
2
(**)
Если продифференцировать F по параметрам и приравнять производные нулю, то получим нелинейную систему нормальных уравнений. В случае линейного уравнения регрессии нормальные уравнения представляли собой систему линейных уравнений, решение которой не составляло труда.
Нелинейный метод наименьших квадратов сводится к задаче минимизации функции (**) нескольких переменных ß=(ß1,…,ßn)
58.Спецификация моделей со случайными возмущениями и преобразование их к системе нормальных уравнений.
Один из принципов спецификации - включение в спецификацию экономической модели случайных возмущений. На практике не всегда удается учесть влияние всех факторов на изучаемую переменную (например, в функции спроса учесть возрастные особенности потребителя), выбрать правильную форму математической зависимости между экономическими переменными (например, нелинейную вместо линейной), безошибочно выполнить измерения (правильно провести опрос). Поэтому необходимо включать некоторые случайные величины, называемые случайные возмущения.
Y = f(x)+ε , где f(x)- часть эндогенной переменной, объясняемая значением экзогенной переменной Х; ε – случайное возмущение. Для того чтобы среди множества уравнений регрессии выбрать одно, необходим критерий отбора. При оценивании параметров регрессионных моделей наиболее часто применяется МНК. Его оценки обладают свойствами несмещённости, состоятельности, эффективности:
(1)
То есть оценки параметров должны быть подобраны таким образом, чтобы сумма квадратов случайных возмущений стремилась к минимуму
(2)
Для нахождения минимума дифференцируем (1):
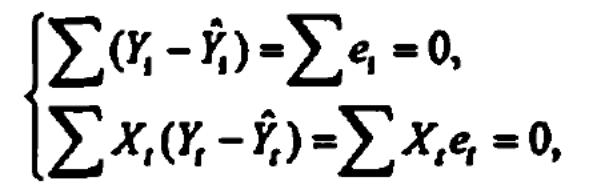
Получаем стандартную форму нормальных уравнений:
Из
которых находим параметры.