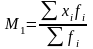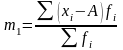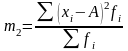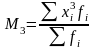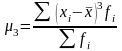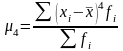Дисперсия альтернативного признака

Альтернативный признак – качественный признак, имеющий две взаимоисключающие разновидности (например, студенты в вузе подразделяются на мужчин и женщин; продукция – на годную и бракованную и т.д.).

Альтернативный признак принимает всего два значения: 1- наличие признака и 0 – отсутствие признака.

Дисперсия альтернативного признака: ,

где р – доли единиц, обладающие данным признаком;

q – доли единиц, не обладающие данным признаком.

Например. На студенческом потоке 40 юношей и 60 девушек. Рассчитайте дисперсию альтернативного признака.

Решение: 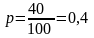; . Следовательно, .

Предельное значение вариации альтернативного признака равно 0,25. Оно получается при

5.4. Моменты распределения

Кроме рассмотренных выше показателей, важной характеристикой рядов распределения являются моменты распределений.

Моментом распределения называется средняя арифметическая из отклонений значений признака от некоторой постоянной величины А в степени k.

В зависимости от того, что принимается за величину А, различают три вида моментов: - начальные моменты получают при А=0;

- центральные моменты получают при А= ;

- условные моменты получают при А не равной средней арифметической и отличной от нуля.

По значению величины k, моменты делятся на моменты 1-го, 2-го и т.д. порядка (табл. 5.1).

Таблица 5.1

Моменты распределения первых четырех порядков

Моменты распределения порядка	Начальные	Центральные	Условные
Первого
Второго
Третьего
Четвертого

Начальный момент 1-го порядка представляет собой среднюю арифметическую и используется как показатель центра распределения.

Центральный момент 2-го порядка представляет собой дисперсию и служит основной мерой колеблемости признака.

Центральный момент 3-го порядка служит для расчета показателя асимметрии.

Центральный момент 4-го порядка применяется при вычислении показателя эксцесса.

Остальные моменты самостоятельного значения не имеют, а используются для упрощения вычислений центральных моментов. Например, используя начальные моменты 1-го и 2-го порядка, можно получить дисперсию:

.

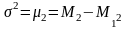5.5. Показатели формы распределения

Выяснение характера распределения предполагает оценку степени его однородности, а также исчисление показателей асимметрии и эксцесса.

В практике статистического исследования приходится встречаться с самыми различными распределениями. Однородные совокупности характеризуются, как правило, одновершинными распределениями. Многовершинность свидетельствует о неоднородности изучаемой совокупности.

Симметричным является распределение, в котором частоты любых двух вариантов, равноотстоящих в обе стороны от центра распределения, равны между собой ( ). Но такое соотношение бывает крайне редко, чаще имеет место, когда частоты располагаются в вариационном ряду сдвинуто в одну или другую сторону.

Для сравнительного анализа степени асимметрии рассчитывают относительный показатель асимметрии:

.

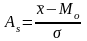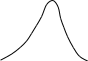
Если , то правосторонняя асимметрия (преобладают варианты меньше средней арифметической; вершина кривой распределения сдвинута влево и правая ветвь вытянута больше, чем левая).

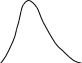
Если , то левосторонняя асимметрия (преобладают варианты больше средней арифметической; вершина кривой распределения сдвинута вправо и левая ветвь вытянута больше, чем правая) (рис. 5.1)

f

f

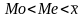
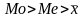
x

x

Рис. 5.1. Асимметричные ряды распределения.

Другой показатель асимметрии, предложенный шведским математиком Линдбергом, исчисляется по формуле: ,

где П – процент тех значений признака, которые превышают величину средней

арифметической.

Наиболее точным и распространенным является показатель асимметрии, исчисляемый по формуле:

.

Чем больше абсолютная величина коэффициента, тем больше степень скошенности. Если 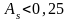(независимо от знака), то асимметрия незначительная, если , то асимметрия значительная.

Оценка степени существенности этого показателя дается с помощью средней квадратической ошибки: , где n – число наблюдений.

Если 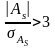, то асимметрия существенна и распределение признака в генеральной совокупности не является симметричным.

Если 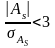, то асимметрия несущественна, ее наличие объясняется влиянием случайных обстоятельств.

Для симметричных распределений рассчитывается показатель эксцесса:

.

Эксцесс – выпад вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения.

При нормальном распределении .

Если , то распределение островершинное.

Если , то распределение плосковершинное (рис. 5.2.).

Островершинное распределение

Нормальное распределение

Нормальное распределение

Плосковершинное распределение

Рис.5.2. Ряды распределения с положительным и

отрицательным эксцессом.

Предельным значением отрицательного эксцесса является значения ; величина положительного эксцесса является величиной бесконечной.

Слишком плоское распределение говорит о том, что у единиц изучаемой совокупности мало общности, они очень разнородны и средняя величина для такой совокупности является не типичной.

Средняя квадратическая ошибка эксцесса исчисляется по формуле:

, где n – число наблюдений.

Для приближенного определения величины эксцесса может быть использована формула Линдберга:

,

где П – процент количества вариант, лежащих в интервале, равном половине среднего квадратического отклонения (в ту или другую сторону от величины средней).