Подготовка данных к анализу. Первичная обработка данных.

Пусть некоторые объекты или явления представляются множеством своих характеристик: X = (X₁, X₂, …, X_j, …X_m).

Матрицу наблюдений можно составить следующим образом:

В практических задачах приходится проводить статистическую обработку данных с целью исключения аномальных наблюдений, подбора однородных совокупностей, удаление дублирующих переменных и т.д.

Выявление и исключение резко выделяющихся наблюдений

Истинность некоторых индивидуальных наблюдений иногда вызывает сомнения, т.к. они резко выделяются на фоне основной массы наблюдений. Такие аномальные наблюдения могут появляться в следствии:

1. обычные колебания выборки обусловленные природой генеральной совокупности;

2. нарушение условий проведения наблюдений;

3. нарушение условий сбора статистических данных;

4. механические ошибки при регистрации данных и подготовки обработки на ЭВМ.

Единственно надежным способом исключения таких наблюдений является тщательное рассмотрение условий при которой они были получены. Если резко выделяющиеся наблюдения связаны с природой самого явления, то его нельзя исключать. Однако содержательный анализ не всегда доступен и в этом случае используется следующая логическая схема:

1. исходя из допущений о природе анализируемой совокупности задаём некоторую функцию  которую называют мерой удалённости от основной массы;

2. этот индикатор является индикатором аномальности. Значение этой функции вычисляются для всех наблюдений и сравнивают их с некоторым пороговым (уставка, норма) значением ₀;

3. Если  < ₀ , то наблюдение остается в совокупности;

4. Для всех наблюдений, для которых  > ₀ они либо исключаются из выборки, либо их значение подавляется с помощью весовых коэффициентов.

Если аномальные наблюдения выделены в группу для отдельного анализа, то все остальные подвергаются сглаживанию.

Для выделения аномальных наблюдений в нормально-распределённых данных применяют статистические критерии.

Рассмотрим каждый столбец матрицы наблюдений как одномерную выборку и представим элементы этого столбца в ранжированном виде, т. е. отсортируем столбец, например, по возрастанию. Тогда числа

х_(1)j 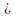x_(2)j … x_(n)j , в этом выражении (1), (2), …,(n) – некоторая подстановка последовательности индексов i=1, …,n.

Составляем следующую комбинацию:

,

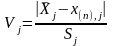, где ,

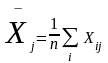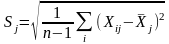
Статистика V_j описывается распределением Стьюдента. Задавшись величиной 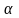- уровень значимости по двум числам , n из таблиц находим величину V_табл. Проверяется неравенство V_j<V_табл. Если неравенство выполняется, то значение x(n)_j остается в выборке. Эта процедура проводится до тех пор, пока не будут отброшены все резковыделяющиеся наблюдения.

Методика полностью справедлива, если числа выборки распределены по нормальному закону. В противном случае этой методикой можно пользоваться, если числа удается каким-либо преобразованием привести к форме нормального распределения (хотя бы приближенно).

Сглаживание кривых

Сглаживание заключается в уточнении ординаты каждой точки с учётом положения нескольких ближайших точек. Часто применяется метод линейного сглаживания по пяти точкам. В этом методе используют 5 формул по две для точек крайних справа и слева и одну для всех внутренних точек.

yS₀ = 0,2(3y₀ + 2y₁ + y₂ – y₄) - крайняя левая точка

yS₁ = 0,1(4y₀ + 3y₁ + 2y₂ + y₃) - следующая точка

yS_n-1 = 0,1(y_n-3 + 2y_n-2 + 3y_n-1 + 4y_n) - предпоследняя точка

yS_n= 0,2(3y_n + 2y_n-1 + y_n-2 – y_n-4) - крайняя правая

Для всех внутренних точек, т.е. таких, что i = 2, …, n-2 применяется:

yS_i= 0,2(y_i-2 + y_i-1 + y_i + y_{i+1 +} y_i+2)

Наиболее часто используется так называемое экспоненциальное сглаживание. При таком сглаживании предполагается что

x_i = b + 

x_i – измерение; b – детерминированное число;  - случайная ошибка.

Константа b относительно стабильна, но может иногда меняться со временем.

Одним из интуитивных способов выделения b, является использование скользящего среднего, в котором последним наблюдениям приписываются большие веса, чем предпоследним. В свою очередь предпоследним приписываются большие веса, чем предыдущим и т.д. Точная формула простого экспоненциального сглаживания имеет следующий вид:

S_i = x_i + (1-)S_i-1

S_i – сглаженное значение

x_i – текущее значение

S_i-1 – предыдущий сглаженный ряд

Когда эта формула применяется рекурсивно, то каждое новое сглаженное значение (которое одновременно является прогнозом) вычисляется как взвешенное среднее текущего наблюдения и сглаженного ряда. Коэффициент сглаживания  выбирается из промежутка [0, 1] по принципу:

(S_i – x_i)²  min

Ряд функций MathCAD предназначены для выполнения сглаживания. В названии этих функций имеется слово Smooth (гладкий).

1: medsmooth (VY, n) − это функция для m -мерного VY возвращает m-мерный вектор сглаженных значений по методу скользящей медианы. n – это ширина окна сглаживания, должно быть нечётным числом n < m.

2: ksmooth (VX, VY, b). VX и VY n-мерные вектора. b – полоса пропускания. Возвращается n-мерный вектор сглаженных VY, вычисленных на основе распределения Гаусса.

3: supSmooth (VX, VY) – эта функция осуществляет линейное сглаживание по принципу k ближайших соседей ( величина k выбирается адаптивно). VX в этих функциях должны быть отсортированы по возрастанию.