1.3. Пространство сигналов

Для проведения анализа сложных сигналов их объединяют по не­которому признаку во множества. Например, такое множество обра­зуют аналоговые детерминированные сигналы. С сигналами при ана­лизе производят различные операции. Их складывают, умножают на числа, вычитают и т. п.

1.3.1. Метрические пространства

Объединив сигналы, обладающие некоторым общим свойством в одно множество, рассматривают отличительные признаки элементов этого множества. Конкретные сигналы интересны лишь в их отношении с другими сигналами множества. Например, отличительными признаками могут быть: энергия, длительность, частота, максимальная амплитуда, число пересечений нулевого уровня. При сравнении каждой паре элементов ставится в соответствие действительное, положительное число, которое трактуется как расстояние между элементами, при этом само множество приобретает геометрические свойства. Множество с определённым на нём расстоянием представляет собой пространство сигналов.

Для определения расстояния необходим функционал, который отображает все пары элементов множества на действительную ось. Такой функционал

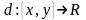
называется метрикой, если он обладает следующими свойствами:

− положительная определённость, симметрия, неравенство треугольника. Множество M с метрикой d называется метрическим пространством (M, d). Разные метрики образуют разные метрические пространства.

Пример 1:

Действительная ось, включающая множество всех действительных чисел, есть метрическое пространство с метрикой

− Это так называемая обычная метрика на R.

Пример 2:

На базе множества Rⁿ упорядоченных последовательностей n действительных чисел (вектор-строк из n чисел)

можно образовать различные пространства с метриками:

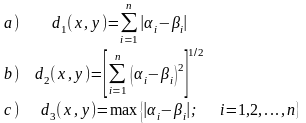
Эти метрики могут быть использованы и на множестве последовательностей комплексных чисел Cⁿ.

1.3.2. Сходимость и непрерывность

Понятие расстояния в метрическом пространстве позволяет анализировать важное свойство бесконечных последовательностей, называемое сходимостью.

Последовательность 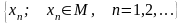сходится, если существует такое , что для любого имеется целое положительное n₀, такое, что

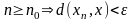
Это часто записывают так:

Любая последовательность, обладающая этим свойством, называется последовательностью Коши. Метрические пространства, в которых все последовательности сходятся, называются полными.

Одно из важных следствий введения метрических пространств состоит в том, что понятие непрерывности может быть обобщено на произвольное отображение одного метрического пространства в другое.

Пусть говорят, что отображение непрерывно в окрестности x₀ если для любого ε>0 существует δ>0 такое, что

,

где y=f(x) и y₀=f(x₀) . Если f непрерывно во всех точках области определения, то говорят, что отображение непрерывно.

Для произвольного множества действительных или комплексных функций времени, заданных на определённом интервале

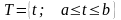
Могут быть определены метрики:

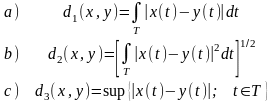
1.3.3. Линейные пространства

Линейное пространство – это множество элементов (называемых векторами) обладающих следующими свойствами.

А. Для каждой пары векторов x, y из рассматриваемого множества имеется вектор (x+y) называемый суммой этих векторов, принадлежащий тому же множеству такой, что:

1. x+y=y+x; сложение коммутативно

2. x+(y+z)=(x+y)+z; сложение ассоциативно

3. x+0=x; для любого вектора существует нулевой и обратный

4. x+(-x)=0

Б. Имеется множество элементов называемых скалярами, которые образуют поле, а также операция умножения на скаляр, ставящая любому вектору x и скаляру α в соответствие α x такая что:

1. α(βx)= αβx; умножение на скаляр ассоциативно

   

2. α(y+x)= αx+ αy; законы

3. (α+β)x= αx+ βx; дистрибутивности

4. 1x= x; 0x=0

Вектор 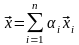− называется линейной комбинацией. Множество векторов называется линейно независимыми, если равенство справедливо только при всех α_i равных нулю.

Любое множество n линейно независимых векторов в M образуют его базисы. Говорят, что M натянуто на базис . Набор чисел является представлением вектора x в Rⁿ или Cⁿ по отношению к базису .