Вейвлет - преобразование

Для анализа сигналов s(t), заданных на всей временной оси , в настоящее время часто используются негармонические базисные функции— вейвлеты (wavelet). Название "вейвлет", переводит­ся на русский язык как "маленькая волна". Вейвлет представляется функцией ψ(t) осциллирующей в некотором временном интервале подобно волне и быстро затухающей вне него. При этом функция должна иметь нулевое среднее значение

На рис. 4 показаны графики двух вейвлетов: мексиканская шляп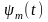а и Хаара .

Общий принцип построения базиса на основе вейвлета состоит в использовании масштабирования (сжатия или растяжения) базис­ной функции во времени и сдвига (смещения) ее по временной оси.

Таким образом, семейство вейвлетов — это функции

,

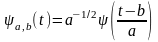где: а — масштаб, b — сдвиг. Коэффициент перед функцией введен для сохранения нормы сигнала в L₂(R).

Чем больше масштаб, тем медленнее изменяется и более «крупномасштабно» выглядит вейвлет. Чем меньше а, тем более высо­кочастотные и быстроизменяющиеся составляющие описывает вейв­лет. Понятие частоты из классического гармонического спектрального анализа в вейвлет-анализе заменено масштабом а.

Используя сдвиг вейвлета, но оси времени, проводим анализ свойств сигнала в разных точках временной оси. Такой сдвиг не пре­дусмотрен в гармоническом анализе. Поэтому вейвлеты удобно ис­пользовать при анализе нестационарных сигналов, когда кроме ин­формации о выявленных частотах нужно получить данные о моментах времени, при которых эти частоты возникают или исчеза­ют.

Непрерывное изменение масштаба а и сдвига b, как правило, яв­ляется избыточным. Для построения вейвлет-рядов можно ограни­читься дискретными значениями а и b, а именно и , где m, - целые (кратномасштабный анализ). Сдвиг b в этом случае про­порционален а. При таком выборе b вейвлеты сдвигаются дискрет­но, малыми шагами, покрывая всю временную ось. В этом случае семейство вейвлетов имеет вид

где т — уровень разрешения, k — целочисленный сдвиг.

Несмотря на дискретность a и b существуют такие ψ(t), которые образуют ортонормированный базис в L₂(R). Например, ортонормированный базис порождает вейвлет Хаара. Легко убедиться, что смешенные и масштабированные функ­ции Хаара ортонормированны. Кроме вейвлетов Хаара ортонормиро­ванный базис образуют вейвлеты Добеши, Симлета, Койфлета, Мейера и др.

Используя ортонормированный базис, получим вейвлет-ряд

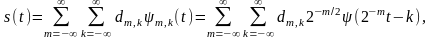
где коэффициенты определяются скалярными произведениями

При фиксированном уровне разре­шения т для представления сигнала используются сдвинутые ко­пии вейвлета с одинаковым масштабом, а = 2^m. При уменьшении уровня разрешения т на 1 используются сжатые вдвое вейвлеты и ряд позволяет описать более высокочастотные составляющие анализируемого сигнала.

Используя скалярное произведение, по аналогии с интегралом Фурье описание сигналов, принадлежащих L₂(R), можно также дать с помощью масштабно-временного непрерывного вейвлет-преобразования (НВП)

(*)

где — вейвлет.

Масштаб и сдвиг изменяются непрерывно. Отметим, что в выражении (4) можно использовать ортогональные, неортогональные и комплексные вейвлеты.

Формулу (*) можно использовать для определения коэффициен­тов d_m,k вейвлет-ряда. Для определения d_m,k достаточно в вместо a и b подставить их дискретные значения.

Для того чтобы обратно получить s(t) из результата масштабно-временного НВП — функции , вейвлет ψ(t) должен допол­нительно удовлетворять следующему условию

где через ψ(ω) обозначено преобразование Фурье для вейвлета ψ(t).

Если условие выполнено, то имеется формула обратного непрерывного вейвлет-преобразования (ОНВП)

Здесь сигнал s(t) выражается через сумму бесконечно большого числа бесконечно малых по величине базисных вейвлетов 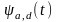с ве­сами .