Фильтр Чебышева второго рода

Функция передачи фильтра Чебышева второго рода связана с функцией передачи фильтра первого рода соотношением:

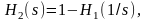
где 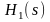и 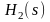– функции передачи фильтров-прототипов Чебышева первого и второго рода соответственно.

АЧХ фильтра описывается следующим образом:

Здесь – частота среза, – порядок фильтра, – полином Чебышева -го порядка, – параметр, определяющий величину пульсаций АЧХ в полосе задерживания.

В результате указанного выше преобразования функции передачи АЧХ фильтра Чебышева второго рода ведет себя так: в полосе пропускания она монотонно затухает, а в полосе задерживания колеблется между нулем и значением . Коэффициент передачи фильтра на нулевой частоте равен 1, на частоте среза – заданному уровню пульсаций в полосе задерживания.

Значение параметра и уровень пульсаций (в децибелах) связаны следующим образом:

дБ,

При 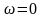АЧХ фильтра Чебышева второго рода является максимально плоской.

На рисунке 3.5 представлена характеристика фильтра:

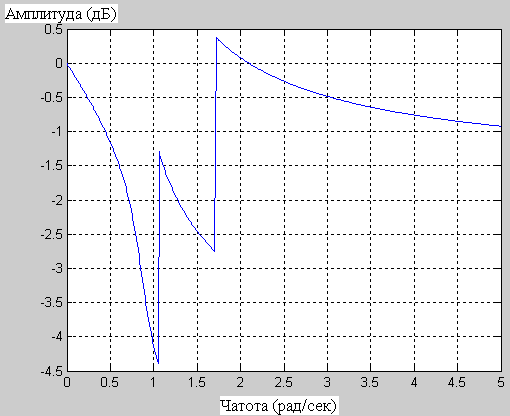
а – АЧХ б – ФЧХ

Рисунок 3.5 – Характеристики фильтра Чебышева с уровнем пульсаций 20 дБ

Эллиптический фильтр

Эллиптические фильтры (фильтры Кауэра) в некотором смысле объединяют в себе свойства фильтров Чебышева первого и второго рода, поскольку АЧХ эллиптического фильтра имеет пульсации заданной величины как в полосе пропускания, так и в полосе задерживания. За счет этого удается обеспечить максимально возможную (при фиксированном порядке фильтра) крутизну ската АЧХ, то есть переходной зоны между полосой пропускания и задерживания.

АЧХ фильтра описывается следующей формулой:

Здесь – частота среза, – порядок фильтра, – рациональная функция Чебышева -го порядка, и – параметры, определяющие величины пульсаций в полосах пропускания и задерживания.

Рисунок 3.6 демонстрирует характеристики эллиптического фильтра с уровнем пульсаций в полосе пропускания 0,5 дБ и уровнем пульсаций в полосе задерживания 20 дБ:

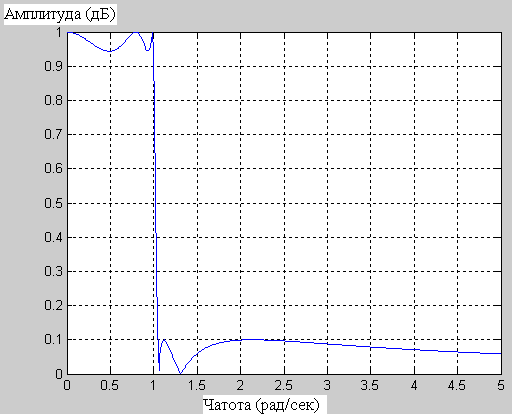
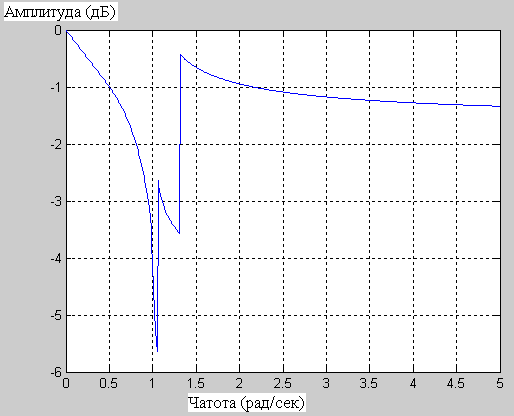
а – АЧХ б – ФЧХ

Рисунок 3.6– Характеристики фильтра с уровнем пульсаций 20 дБ

Фильтр Бесселя

В отличие от предыдущих типов, фильтры Бесселя не аппроксимируют прямоугольную АЧХ – их АЧХ по форме близка к гауссовой кривой (стремится к ней с ростом порядка фильтра). Практическая ценность фильтров Бесселя определяется тем, что для них зависимость группового времени задержки от частоты является максимально гладкой в точке , и групповая задержка мало меняется в полосе пропускания.

Сама функция передачи имеет следующий вид:

Коэффициенты полинома знаменателя рассчитываются по формуле:

На рисунке 3.7 показаны АЧХ и ФЧХ фильтра Бесселя:

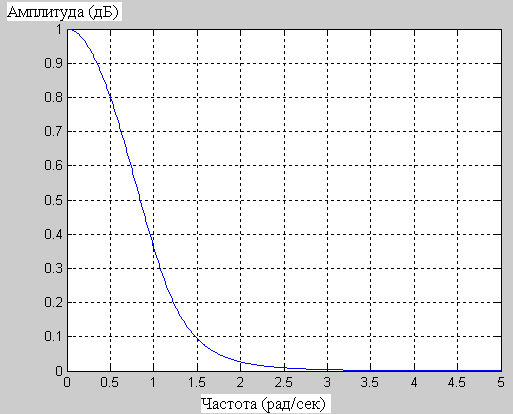
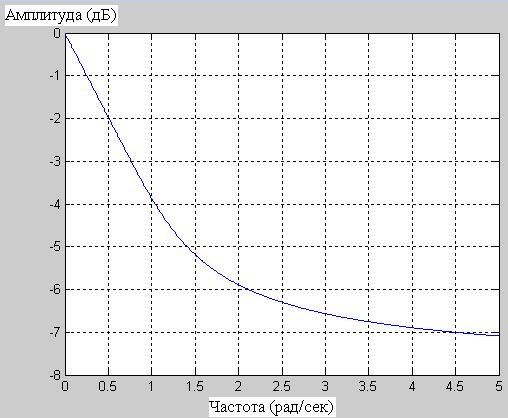
а – АЧХ б – ФЧХ

Рисунок 3.7 – Характеристики фильтра Бесселя

В инженерной практике наиболее часто применяются фильтры Баттерворта и Чебышева.

При исследовании процессов приходится обрабатывать огромные массивы данных, поэтому важно выбрать обоснованную частоту дискретизации и объем выборки. Спектральный анализ позволяет нам оценить эти величины.

Минимальная требуемая частота дискретизации определяется из теоремы Котельникова: для того, чтобы в дискретизированном сигнале можно было выявить гармоники с частотой , частота дискретизации должна быть не менее 2.

При определении минимального объема выборки следует также учесть, что требуется не допустить наложения спектра исследуемого сигнала со спектром модуляции. При этом надо помнить, что частота дискретизации в основном определяет динамические погрешности при аналого-цифровом преобразовании.

Требуемая для обработки длительность сигнала не менее T=Nt, где N - объем выборки. Спектральное разрешение:

.

Для устранения наложений сигнал предварительно пропускают через физический (т.е. реализованный аппаратно, а не программно) фильтр нижних частот, частота среза которого равна частоте Найквиста. Частотная характеристика фильтра должна иметь в этой области крутой излом, однако требования к крутизне уменьшаются по мере уменьшения максимальной частоты спектра сигнала, когда частота дискретизации превышает частоту Найквиста. Но с увеличением частоты дискретизации растет объем выборки. В итоге, исходя из вычислительной мощности аппаратного комплекса (скорости процессора и объема оперативной памяти) можно определить такую частоту и время сбора данных, которые определят приемлемый объем выборки.