Исследование данных на однородность

Данные собираются на разных объектах в разных условиях, поэтому возникает необходимость установления их принадлежности одной генеральной совокупности. Без применения инструментов математической статистики можно решить следующие задачи.

Задача №1.

На матрице исходных данных X сгруппировать данные в однородные группы. Если границы этих групп заданы, то мы имеем задачу классификации. Если границы групп не заданы, то мы имеем задачу распознавания образов.

Решение задачи №1.

Матрицу наблюдений X разобьем на группы с помощью какого-либо метода многомерной классификации. Чаще всего используют так называемые Гиперсферические классы, основанные на Евклидовой метрике. Такие классы называют таксонами.

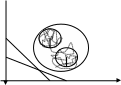
В результате можно получить следующую информацию:

1 − радиус гиперсферы, которая охватывает все множество точек наблюдения;

2 − координаты центра всего исходного множества;

3 − вычисленное или заданное число групп. Радиус, номер координаты центра группы, а так же номера точек попавших в эту группу.

Устанавливается последовательность типичных точек группы, т.е. таких которые наиболее приближены к центру таксона. Для этого обычно исследуются следующие метрики:

1. Евклидовы метрики: d_AB = inf d (X_i , X_j)

в евклидовой метрике выбирается наименьшее значение, распределенное между значениями X_i и X_j

2. использование корреляции: d_AB =1 -‌‌‌ |r_AB|

r – коэффициент корреляции между векторами A и B.

3. медианное расстояние: d_M =median[ | (A-B) – median (A-B) | ].

Задача №2. задача уменьшения размерности.

На первой стадии изучения объектов или явлений рассматриваются все измеряемые факторы, так чтобы сформировать матрицу исходных данных X максимальной размерности. Затем группировкой пытаемся уменьшить размер этой матрицы. Для этого выделяем однородные группы и в них оставляем 1 – 2 фактора.

Решение задачи№2.

Проводится группировка в m факторах для k классов. Например: с помощью метрики: d=1 - │r_jk│. После образования т.о. групп факторов выбираем из каждой группы по одному, максимально по два фактора. Обычно при этом придерживаются следующих рекомендаций:

1) чем ближе фактор к среднему группы, тем предпочтительней его выбор;

2) выбирается фактор имеющий наибольший коэффициент корреляции с зависимой переменной;

3) связь отобранного фактора с другими переменными должна быть наименьшей.

Исследование данных на однородность может быть проведено средствами математической статистики.

Пусть имеются две выборки нормально распределённых случайных чисел ; ; ; .

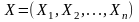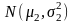Проверяется гипотеза для этого формируется комплекс

,

где ,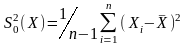

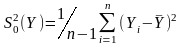
Если верна H₁, то ρ (X,Y) имеет распределения Фишера F_n-1,m-1 с n-1, m-1 степенями свободы. Если 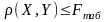, то эти выборки принадлежат одной генеральной совокупности.

Диагностика мультиколлинеарности

Одно из основных предположений, относящихся к матрице исходных данных X, состоит в следующем. Среди независимых переменных не должно быть линейно зависимых. Однако на практике наблюдается часто сильная корреляционная зависимость между столбцами этой матрицы. Крайний случай возникает тогда, когда некоторые столбцы или даже все связаны линейной зависимостью, т.е. V₁X₁ + V₂X₂ + … + V_pX_p = 0

X_j – j-тый столбец X, V_j – некоторые числа удовлетворяющие условию:

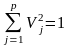2  p  m

В этом случае говорят, что присутствует мультиколлинеарность. Отрицательные последствия мультиколлинеарности:

• падает точность оцениваемых параметров модели, дисперсии коэффициентов становятся большими и сильно коррелируют друг с другом;

• из-за корреляции коэффициентов модели, трудно установить истинное влияние соответствующей независимой переменной на зависимую;

• оценки коэффициентов модели становятся чувствительными к объему исходных данных, так что, добавление совсем небольшого числа наблюдений, приводит к сильным сдвигам в значениях некоторых коэффициентов модели.

Преобразуем матрицу X так, чтобы по столбцам выполнялись следующие равенства:

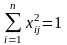(j = 1…m)

Переменные полученные в результате таких преобразований называются нормализованными переменными, а матрица R = Q^T_норм.  Q_норм. Называется корреляционной матрицей. Если столбцы линейно независимы, т.е. X^T_j  X_k = 0 для jk , то в этом случае det R = 1 (determinant). Если же линейно зависимы, т.е. столбцы коллинеарны, то det R = 0.

Выход из тупика мультиколлинеарности состоит в формировании банка новых данных или в разработке специальных методов оценки значений коэффициентов модели. Наиболее простой способ устранения мультиколлинеарности это исключение из каждой пары переменной, той которая с другими переменными имеет коэффициент корреляции > 0,8. при этом оставляют те переменные которые обладают большей ценностью с точки зрения интерпретации.