14 Вопрос

Пло́тность вероя́тности — один из способов задания вероятностной меры на евклидовом пространстве  . В случае, когда вероятностная мера является распределением случайной величины, говорят о плотности случайной величины.

Пусть   является вероятностной мерой на  , то есть определено вероятностное пространство  , где   обозначает борелевскую σ-алгебру на  . Пусть  обозначает меру Лебега на  .

Определение 1. Вероятность   называется абсолютно непрерывной (относительно меры Лебега) ( ), если любое борелевское множество нулевой меры Лебега также имеет вероятность ноль:

Если вероятность   абсолютно непрерывна, то согласно теореме Радона-Никодима существует неотрицательная борелевская функция   такая, что

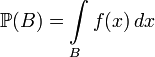,где использовано общепринятое сокращение  , и интеграл понимается в смысле Лебега.

Определение 2. В более общем виде, пусть   — произвольное измеримое пространство, а   и   — две меры на этом пространстве. Если найдется неотрицательная  , позволяющая выразить меру   через меру   в виде

то такую функцию называют плотностью меры   по мере  , или производной Радона-Никодима меры   относительно меры  , и обозначают

.

Свойства плотности вероятности

• Плотность вероятности определена почти всюду. Если   является плотностью вероятности   и  почти всюду отн 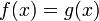осительно меры Лебега, то и функция 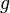  также является плотностью вероятности  .

• Интеграл от плотности по всему пространству равен единице:

.

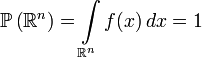Обратно, если   — неотрицательная п.в. функция, такая что 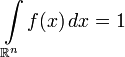 , то существует абсолютно непрерывная вероятностная мера   на   такая, что   является её плотностью.

• Замена меры в интеграле Лебега:

,

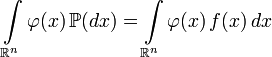где   любая борелевская функция, интегрируемая относительно вероятностной меры  .

Плотность случайной величины

Пусть определено произвольное вероятностное пространство  , и   случайная величина (или случайный вектор).   индуцирует вероятностную меру   на  , называемую распределением случайной величины  .

Определение 3. Если распределение   абсолютно непрерывно относительно меры Лебега, то его плотность   называется плотностью случайной величины  . Сама случайная величина   называется абсолютно непрерывной.

Таким образом для абсолютно непрерывной случайной величины имеем:

.

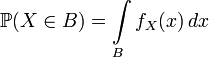Замечания

• Не всякая случайная величина абсолютно непрерывна. Любое дискретное распределение, например, не является абсолютно непрерывным относительно меры Лебега, а потому дискретные случайные величины не имеют плотности.

• Функция распределения абсолютно непрерывной случайной величины   непрерывна и может быть выражена через плотность следующим образом:

.

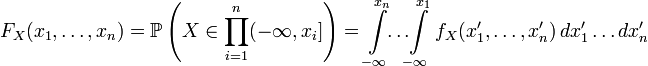В одномерном случае:

.

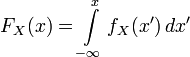Если  , то  , и

.

В одномерном случае:

.

• Математическое ожидание функции от абсолютно непрерывной случайной величины может быть записано в виде:

,

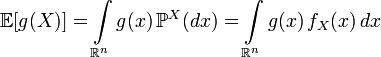где   — борелевская функция, так что   определено и конечно.

Плотность преобразования случайной величины

Пусть   — абсолютно непрерывная случайная величина, и   — инъективная непрерывно дифференцируемая функция такая, что  , где   — якобиан функции   в точке  . Тогда случайная величина   также абсолютно непрерывна, и её плотность имеет вид:

.

В одномерном случае:

.
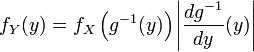