5Вопрос

Теорема умножения вероятностей

Произведением   двух  событий   А   и   Вназывают событие АВ, состоящее в совместном появлении (совме­щении) этих событий.

Например. Событие А-деталь годная, Событие В-деталь окрашенная, то Событие АВ - деталь годна и окрашена.

Произведением нескольких событий называют событие, состоящее в совместном появлении всех этих событий.

Например. События А, В, С-появление "герба" соответственно в первом, втором и третьем бросаниях монеты, то событие АВС - выпадение "герба" во всех трех испытаниях.

Рассмотрим два события: А и В; пусть вероят­ности Р(А) и Р_А(В) известны. Чтобы найти вероятность совмещения этих событий, т. е. вероятность того, что появиться и событие А и событие В необходимо воспользоваться следующей теоремой:.

Теорема. Вероятность совместного появления двух со­бытий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило;

Следствие. Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появи­лись:

 

6 Вопрос

Теорема сложения вероятностей формулируется следующим образом.

Вероятность суммы двух несовместимых событий равна сумме вероятностей этих событий:

.      (3.2.1)

Докажем теорему сложения вероятностей для схемы случаев. Пусть возможные исходы опыта сводятся к совокупности случаев, которые мы для наглядности изобразим в виде n точек:

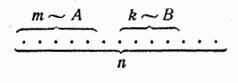
Предположим, что из этих случаев   благоприятны событию , а  – событию . Тогда

Так как события   и  несовместимы, то нет таких случаев, которые благоприятны и , и  вместе. Следовательно, событию   благоприятны   случаев и

Подставляя полученные выражения в формулу (3.2.1), получим тождество. Теорема доказана.

Обобщим теорему сложения на случай трех событий. Обозначая событие   буквой  , и присоединяя к сумме еще одно событие  , легко доказать, что

Очевидно, методом полной индукции можно обобщить теорему сложения на произвольное число несовместных событий. Действительно, предположим, что она справедлива для n событий:

и докажем, что она будет справедлива для   событий:

Обозначим:

Имеем:

.

Но так как для n событий мы считаем теорему уже доказанной, то

,

откуда

,

что и требовалось доказать.

Таким образом, теорема сложения вероятностей применима к любому числу несовместных событий. Её удобнее записать в виде:

.                   (3.2.2)

Отметим следствия, вытекающие из теоремы сложения вероятностей.

Следствие 1. Если события   образуют полную группу несовместных событий, то сумма их вероятностей равна единице:

.

Доказательство. Так как события   образуют полную группу, то появление хотя бы одного из них – достоверное событие:

.

Так как   - несовместные события, то к ним применима теорема сложения вероятностей

,

откуда

,

что и требовалось доказать.

   Перед тем как вывести второе следствие теоремы сложения, определим понятие о «противоположных событиях».

Противоположными событиями называются два несовместных события, образующих полную группу.

Событие, противоположное событию  , принято обозначать  .

Примеры противоположных событий.

1)   – попадание при выстреле,   - промах при выстреле;

2)  – выпадение герба при бросании монеты,   - выпадение цифры при бросании монеты;

3)  – безотказная работа всех элементов технической системы,   - отказ хотя бы одного элемента;

4)  – обнаружение не менее двух бракованных изделий в контрольной партии,   - обнаружение не более одного бракованного изделия.

Следствие 2. Сумма вероятностей противоположных событий равна единице:

.

Это следствие есть частный случай следствия 1. Оно выделено особо ввиду его большой важности в практическом применении теории вероятностей. На практике весьма часто оказывается легче вычислить вероятность противоположного события  , чем вероятность прямого события  . В этих случаях вычисляют   и находят  .