20 Вопрос

Регре́ссия (лат. regressio — обратное движение, отход), в теории вероятностей и математической статистике, зависимость среднего значения какой-либо величины от некоторой другой величины или от нескольких величин. В отличие от чисто функциональной зависимости y=f(x), когда каждому значению независимой переменной x соответствует одно определённое значение величины y, при регрессионной связи одному и тому же значению x могут соответствовать в зависимости от случая различные значения величины y. Если при каждом значении x=x_i наблюдается n_i значений y_i1…y_in1 величины y, то зависимость средних арифметических  =(y_i1+…+y_in1)/n_i от x=x_i и является регрессией в статистическом понимании этого термина^[1

Регрессия может быть прямой (b>0) и обратной (b<0). Прямая регрессия означает, что при росте одного параметра, значения другого параметра тоже увеличиваются. А обратная, что при росте одного параметра, значения другого параметра уменьшаются.

21 Вопрос

Зако́н больши́х чи́сел в теории вероятностей утверждает, что эмпирическое среднее (среднее арифметическое) достаточно большой конечной выборки из фиксированного распределения близко к теоретическому среднему (математическому ожиданию) этого распределения. В зависимости от вида сходимости различают слабый закон больших чисел, когда имеет место сходимость по вероятности, и усиленный закон больших чисел, когда имеет место сходимость почти всюду.

Всегда найдётся такое количество испытаний, при котором с любой заданной наперёд вероятностью относительная частота появления некоторого события будет сколь угодно мало отличаться от его вероятности.

Общий смысл закона больших чисел — совместное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая.

На этом свойстве основаны методы оценки вероятности на основе анализа конечной выборки. Наглядным примером является прогноз результатов выборов на основе опроса выборки избирателей.

Формула Бернулли

Пусть проводятся независимые испытания (такие, при которых вероятность появления события в каждом испытании не зависит от результатов предыдущих испытаний). Далее, вероятность наступления интересующего нас события в каждом испытании постоянна и равна p. Тогда вероятность того, что рассматриваемое событие появится ровно k раз при n испытаниях (безразлично, в каком порядке), равна

В формуле Бернулли используется число сочетаний. Повторюсь, что для реализации схемы Бернулли необходимы два условия: 1) независимость проводимых испытаний; 2) p = const (постоянное значение вероятности появления события) Распределение вероятностей в схеме Бернулли - биномиальное. Наивероятнейшее число появления события (мода) при n испытаниях заключено в пределах np-q ≤ Mo ≤ np+p, В данном   мы докажем одну из простейших, но вместе с тем наиболее важных форм закона больших чисел - теорему Чебышева. Эта теорема устанавливает связь между средним арифметическим наблюденных значений случайной величины и ее математическим ожиданием. Запишем в аналогичной форме теорему Чебышева. Она утверждает, что при увеличении   среднее арифметическое   сходится по вероятности к  , т. е.

.             (13.3.1)

Докажем это неравенство.

Доказательство. Выше было показано, что величина

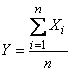
имеет числовые характеристики

;  .

Применим к случайной величине   неравенство Чебышева, полагая  :

.

Как бы мало ни было число  , можно взять   таким большим, чтобы выполнялось неравенство

где   - сколь угодно малое число.

Тогда

,

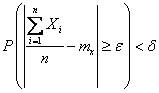откуда, переходя к противоположному событию, имеем:

,

что и требовалось доказать.

 Теорема Ляпунова - Пусть с  ,… последовательность попарно независимых случайных величин с математическими ожиданиями M  и дисперсиями D  , причём эти величины обладают следующими двумя свойствами:

1) Cуществует такое число L, что для любого i имеет место неравенство  , т, е. все значения случайных величин, как говорят, равномерно ограничены, относительно математических ожиданий;

2) Сумма   неограниченно растёт при 

Тогда при достаточно большом n сумма   имеет распределение, близкое к нормальному.

Пусть   и   математическое ожидание и дисперсия случайной величины  . Тогда

Где   — интеграл вероятности.Ξερω/