1 Вопрос

Для начала, возьмем в руки монетку, будем ее бросать и записывать результат последовательно в виде строки: О, Р, Р, О, О, Р. Здесь буквами О и Р обозначено выпадение орла или решки. В нашем случае бросание монетки – это испытание, а выпадение орла или решки – событие, то есть возможный исход нашего испытания.

Пусть мы провели испытание N раз, R раз выпала решка, O = N – R раз выпал орел.

Предположим, что при большом числе испытаний N отношение   стремится к некоторой постоянной величине. Назовём её вероятностью p наступления события.

Если существует идеализированный процесс, который можно представить в виде испытаний, и частота случайного события приближается к пределу 

. то этот предел называется вероятностью данного случайного события

Часто вероятность, которая в нашем определении заключена в интервале 0 ≤ p ≤ 1, выражают в процентах, умножая число p на 100 %.

Иногда вероятность события можно предсказать из соображений симметрии. Например, при бросании «идеального» игрального кубика выпадение любой грани равновозможно (равновероятно). Всего граней 6, значит, вероятность выпадения i-й грани p (A_i) = p (A₁) = p (A₂) = p (A₃) = p (A₄) = p (A₅) = p (A₆) = 1/6.

Если мы имеем дело с измеримыми случайными величинами, например, измеряем в течение нескольких лет количество снега, выпавшего за день, то понятие вероятности тоже можно ввести. Для этого запишем результаты измерения в таблицу с точностью, например, в сантиметр и подсчитаем относительную частоту появления того или иного значения. Например, вероятность того, что выпадет 3 см снега, – 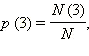  где N (3) – количество дней, в каждый из которых выпало 3 см, N – общее количество дней, в которые проводились измерения.

Для того чтобы найти вероятность события A, происходящего в серии испытаний, нужно:

1. найти число N всех возможных исходов (элементарных событий);

2. принять предположение о равновероятности этих исходов;

3. найти количество N (A) тех исходов, в которых наступает событие A;

4. найти частное 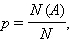  оно и будет равно вероятности p (A) наступления события A.

В этой очевидной инструкции есть очень важный пункт о равновероятности исходов. Проиллюстрируем его на примерах.

2 Вопрос

События подразделяются на: достоверные, возмож­ные (или случайные) и невозможные.

Достоверным называется такое событие, которое в результате опыта непременно должно произойти.

Возможным или случайным называется событие, которое может появиться в результате опыта, но может и не появиться. Приведенные на стр. 7 примеры собы­тий (1—8) все являются случайными.

Два или несколько событий  называются  равновозможными, если нет оснований утверждать, что одно из них объективно имеет больше данных появиться в итоге опыта по сравнению с другими. Например, вы­падение герба и выпадение цифры при однократном бросании монеты; выпадения 1, 3 и 5 очков при бросании игральной кости; выход из строя любой из однотипных радиоламп, работающих в одинаковых условиях и вклю­ченных в одно и то же время.

По характеру взаимной связи события подразделя­ются на совместимые (или, как иногда говорят, совмест­ные) и .несовместимые (несовместные).

События называются несовместимыми, если по­явление какого-либо одного из них в данном опыте исключает возможность появления других. Например, выпадения 3 и 5 очков вместе при однократном бро­сании игральной кости (может выпасть либо 3, либо 5 очков).

События называются совместимыми, если появ­ление одного из них в данном опыте не исключает возможности появления других.

Примеры. Выпадение 3 и 5 очков при двукратном бро­сании игральной кости; искажение различных знаков при передаче радиограммы.

Группа событий, из которых хотя бы одно непре­менно должно произойти в данном опыте, называется полной группой событий.

События, составляющие полную группу, называются единственно возможными в данном опыте собы­тиями (никакие другие события   в  данном опыте произойти не могут).

Единственно возможные события могут быть совме­стимыми и несовместимыми.

Два единственно возможных и несовместимых собы­тия называются противоположными.