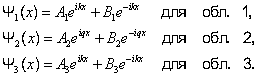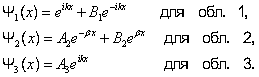- •1.Закономерности излучения черного тела. Законы Кирхгофа, Стефана-Больцмана, Вина. Формула Рэлея-Джинса. Ультрафиолетовая катастрофа.
- •2.Энергия и импульс фотона. Формула Планка для спектра излучения черного тела.
- •3.Квантовая теория фотоэффекта. Эффект Комптона.
- •4.Давление света. Опыты, подтверждающие давление света. Корпускулярно-волновой дуализм излучения.
- •6.Волновой пакет микрочастицы. Соотношение неопределенностей Гейзенберга.
- •7.Опыты Резерфорда по рассеянию -частиц. Формула Резерфорда. Модель атома Резерфорда-Бора.
- •8.Закономерности в спектрах атома водорода. Серии Лаймана, Бальмера, Пашена. Комбинационный принцип Ритца.
- •9.Дискретность квантовых состояний атома. Постулаты Бора. Опыты Франка-Герца.
- •10.Спонтанные и вынужденные переходы. Коэффициенты Эйнштейна. Спектральная плотность излучения.
- •11.Принцип работы лазера. Типы лазеров. Свойства лазерного излучения.
- •12. Волновая функция микрочастицы и ее свойства. Стационарное и нестационарное уравнение Шредингера.
- •13. Решение уравнения Шредингера для свободной микрочастицы и находящейся в потенциальной яме.
- •14. Прохождение микрочастицы через потенциальный барьер. Туннельный эффект.
- •15. Гармонический осциллятор. Квантомеханическое описание атома водорода.
- •16. Уровни энергии и схема термов щелочных металлов. Дублетная структура спектров щелочных металлов.
- •17. Магнитный и механический моменты электронов. Спин. Опыты Штерна и Герлаха.
- •18. Результирующий механический момент многоэлектронного атома. J-j и l-s связь.
- •19. Нормальный и аномальный эффекты Зеемана. Фактор Ланде.
- •20. Электронные оболочки атома и их заполнение. Принцип Паули. Правила Хунда.
- •21. Тормозное и характеристическое рентгеновское излучение. Закон Мозли.
- •22. Физические особенности в молекулярных спектрах. Энергия и спектр двухатомной молекулы. P-, q- и r-ветви.
- •23. Одномерный кристалл Кронига-Пенни. Понятие о зонной теории твердых тел. Распределения Ферми-Дирака и Бозе-Эйнштейна. Фермионы и бозоны.
- •Теория бкш(теория Бардина-Купера-Шриффера) -
14. Прохождение микрочастицы через потенциальный барьер. Туннельный эффект.
Рассмотрим простейший потенциальный барьер прямоугольной формы (рис. 5.4) для одномерного (по оси х) движения частицы.
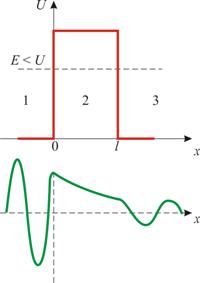
Рис. 5.4
Для потенциального барьера прямоугольной формы высоты U и ширины l можно записать:
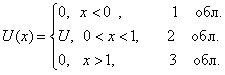
При данных условиях задачи классическая частица, обладая энергией Е, либо беспрепятственно пройдет над барьером при E>U, либо отразится от него (E<U) и будет двигаться в обратную сторону, т.е. она не может проникнуть через барьер.
Для микрочастиц же, даже при E<U, имеется отличная от нуля вероятность, что частица отразится от барьера и будет двигаться в обратную сторону. При E>U имеется также отличная от нуля вероятность, что частица окажется в области x>l, т.е. проникнет сквозь барьер. Такой вывод следует непосредственно из решения уравнения Шредингера, описывающего движение микрочастицы при данных условиях задачи.
Уравнение Шредингера для состояний каждой из выделенных областей имеет вид:
|
|
(5.4.1) |
|
|
|
(5.4.2) |
|
Общее решение этих дифференциальных уравнений:
|
|
(5.4.3) |
|
В
данном случае, согласно (5.4.2),
![]() –
мнимое число, где
–
мнимое число, где
![]()
Можно показать, что A1 = 1, B3 = 0, тогда, учитывая значение q,получим решение уравнения Шредингера для трех областей в следующем виде:
|
|
(5.4.4) |
|
В области 2 функция (5.4.4) уже не соответствует плоским волнам, распространяющимся в обе стороны, поскольку показатели степени не мнимые, а действительные.
Качественный анализ функций Ψ1(x), Ψ2(x), Ψ3(x) показан на рис. 5.4. Из рисунка следует, что волновая функция не равна нулю и внутри барьера, а в области 3, если барьер не очень широк, будет опять иметь вид волн де Бройля с тем же импульсом, т.е. с той же частотой, но с меньшей амплитудой.
Таким образом, квантовая механика приводит к принципиально новому квантовому явлению –туннельному эффекту, в результате которого микрообъект может пройти через барьер.
Коэффициент
прозрачности для барьера прямоугольной
формы
![]() .
.
Для
барьера произвольной формы
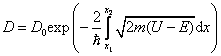 .
.
Прохождение
частицы сквозь барьер можно пояснить
соотношением неопределенностей.
Неопределенность импульса на отрезке
Δx
= l
составляет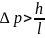 Связанная с этим разбросом кинетическая
энергия
Связанная с этим разбросом кинетическая
энергия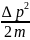 может оказаться достаточной для того,
чтобы полная энергия оказалась больше
потенциальной и частица может пройти
через барьер. С
классической точки зрения прохождение
частицы сквозь потенциальный барьер
при E<U
невозможно, так как частица, находясь
в области барьера, должна была бы обладать
отрицательной кинетической энергией.
Туннельный эффект является специфическим
квантовым эффектом.Оказывается,
что можно обнаружить частицу за пределами
дозволенной (рис. 5.5), т.е. за точками 0 и
l(рис.
5.1).
может оказаться достаточной для того,
чтобы полная энергия оказалась больше
потенциальной и частица может пройти
через барьер. С
классической точки зрения прохождение
частицы сквозь потенциальный барьер
при E<U
невозможно, так как частица, находясь
в области барьера, должна была бы обладать
отрицательной кинетической энергией.
Туннельный эффект является специфическим
квантовым эффектом.Оказывается,
что можно обнаружить частицу за пределами
дозволенной (рис. 5.5), т.е. за точками 0 и
l(рис.
5.1).
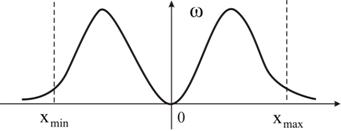
Рис. 5.5
Это означает, что частица может прибывать там, где ее полная энергия меньше потенциальной энергии. Это оказывается возможным вследствие туннельного эффекта.