54. Дифферинциальное уравнение свободных затухающих коллебаинй и его решение.

Решение уравнения (1) запишем в виде   (2)  где u=u(t). После взятия первой и второй производных (2) и подстановки их в выражение (1) найдем   (3)  Решение уравнения (3) зависит от знака коэффициента перед искомой величиной. Рассмотрим случай положителньного коэффициента:   (4)  (если (ω₀² - σ²)>0, то такое обозначение мы вправе сделать). Тогда получим выражение   , у которого решение будет функция   . Значит, решение уравнения (1) в случае малых затуханий (ω₀² >> σ² )   (5)  где   (6) — амплитуда затухающих колебаний, а А₀ — начальная амплитуда. 

55. Механические гармонические колебания. Гармонический осциллятор. Пружинный, физический и математический маятники.

Механическое гармоническое колебание - это прямолинейное неравномерное движение, при котором координаты колеблющегося тела (материальной точки) изменяются по закону косинуса или синуса в зависимости от времени.

Гармони́ческий осцилля́тор (в классической механике) — система, которая при смещении из положения равновесия испытывает действие возвращающей силы F, пропорциональной смещению x (согласно закону Гука):

Пружинный маятник — это груз массой т, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы F = –kx, где k — жесткость пружины. Уравнение движения маятника

Физический маятник — это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси, проходящей через точку О, не совпадающую с центром масс С тела.

Математический маятник — это идеализированная система, состоящая из материальной точки массой т, подвешенной на нерастяжимой невесомой нити, и колеблющаяся под действием силы тяжести

56. Сложение гармонических колебаний одного направления и одинаковой частоты. Биения.

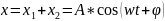
Биения наблюдаются в случае сложения двух гармонических колебаний оного направления с одинаковыми амплитудами, частоты которых немного отличаются друг от друга.

57. Сложение взаимно-перпендикулярных колебаний.

58. Волновое движение. Плоская бегущая волна.

Волновой процесс (волна)—это процесс распространения колебаний в сплошной среде. Сплошная среда — непрерывно распределенная в пространстве и обла­дающая упругими свойствами.

Бегущие волны – волны, которые переносят в пространстве энергию.

Плоские волны – волны, волновые поверхности которых – есть совокупность параллельных плоскостей, перпендикулярных направлению распространения волны.

Уравнение плоской бегущей волны.

59. Уравнение плоской волны.

60. Фазовая и групповая скорость.

Фазовая скорость - скорость, с которой распространяется поверхность одинаковых фаз.

Групповая скорость — это величина, характеризующая скорость распространения «группы волн» - то есть более или менее хорошо локализованной квазимонохроматической волны (волны с достаточно узким спектром).

61. Интерференция волн. Образование стоячих волн.

Интерференция волн — взаимное увеличение или уменьшение результирующей амплитуды двух или нескольких когерентных волн, одновременно распространяющихся в пространстве.