3. Законы Ньютона:

1. Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальная точка при отсутствии внешних воздействий сохраняет величину и направление своей скорости неограниченно долго.

2. В инерциальной системе отсчёта ускорение, которое получает материальная точка, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе.

3. Действию всегда есть равное и противоположное противодействие.

4. Силы трения, притяжения, упругие.

1. Сила притяжени или гравита́ция (всеми́рное тяготе́ние, )— универсальное фундаментальное взаимодействие между всеми материальными телами. 

7. Энергия. Работа. Закон сохранения энергии.

1. Энергия  — скалярная физическая величина, являющаяся единой мерой различных форм движения и взаимодействия материи, мерой перехода движения материи из одних форм в другие.

2. Механическая работа — это физическая величина, являющаяся скалярной количественной мерой действия силы или сил на тело или систему, зависящая от численной величины, направления силы (сил) и от перемещения точки (точек) тела или системы

3. Зако́н сохране́ния эне́ргии — фундаментальный закон природы, установленный эмпирически и заключающийся в том, что для изолированной физической системы может быть введена скалярная физическая величина, являющаяся функцией параметров системы и называемая энергией, которая сохраняется с течением времени. 

8. Консервативные силы. Потенциальная энергия во внешнем поле сил.

1. Консервати́вные си́лы (потенциальные силы) — силы, работа которых не зависит от формы траектории (зависит только от начальной и конечной точки приложения сил)

2. Потенциальная энергия  — скалярная физическая величина, характеризующая способность некого тела (или материальной точки) совершать работу за счет своего нахождения в поле действия сил.

   1. О физическом смысле понятия потенциальной энергии

      1. Если кинетическая энергия может быть определена для одного отдельного тела, то потенциальная энергия всегда характеризует как минимум два тела или положение тела во внешнем поле.

      2. Кинетическая энергия характеризуется скоростью; потенциальная — взаиморасположением тел.

      3. Основной физический смысл имеет не само значение потенциальной энергии, а её изменение.

10 Момент импульса и закон его сохранения

Моме́нт и́мпульса характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.

Зако́н сохране́ния и́мпульса (Зако́н сохране́ния количества движения) утверждает, что векторная сумма импульсов всех тел (или частиц)замкнутой системы есть величина постоянная.

11 Условия равновесия механической системы

Механи́ческое равнове́сие — состояние механической системы, при котором сумма всех сил, действующих на каждую её частицу, равна нулю и сумма моментов всех сил, приложенных к телу относительно любой произвольно взятой оси вращения, также равна нулю.

12. Абсолютно неупругий удар. Абсолютно упругий удар.

Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело.

Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел. 

13.Вращение тела вокруг неподвижной оси.

При вращательном движении тела вокруг неподвижной оси все его точки, лежащие на оси вращения, остаются неподвижными. Остальные точки вращающегося тела описывают окружности вокруг неподвижной оси в плоскостях, перпендикулярных к оси, с центром на этой оси.

14.Момент инерции тела. Расчет момента инерции некоторых тел.

Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. 

15. Теорема Гюйгенса-Штайнера.

Теоре́ма Гю́йгенса — Ште́йнера: момент инерции тела   относительно произвольной оси равен сумме момента инерции этого тела   относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела   на квадрат расстояния   между осями:

где

 — известный момент инерции относительно оси, проходящей через центр масс тела,

 — искомый момент инерции относительно параллельной оси,

 — масса тела,

 — расстояние между указанными осями.

16. Работа и кинетическая энергия тела при вращении.

Работа при вращении тела равна произведению момента действующей силы на угол поворота.  dA = M_zdφ

Кинетическая энергия вращающегося тела есть сумма кинетических энергий его точек.

17. Уравнение динамики вращательного движения твердого тела.

Произведение момента инерции тела на его угловое ускорение равно суммарному моменту внешних сил, действующих на тело. Моменты сил и инерции берутся относительно оси, вокруг которой происходит вращение. M_z = I_z·. 

18. Гироскопы. Свободные оси.

Гироскопы — массивные однородные тела, вращающиеся с большой угловой скоростью около своей оси симметрии, являющейся свободной осью.

Существуют такие оси вращения тел, которые не изменяют своей ориентации в пространстве без действия на нее внешних сил эти оси называются свободными осями.

19. Прецессионное движение оси гироскопа.

Устойчивость оси свободного гироскопа дает возможность использовать его в качестве прибора для обнаружения суточного вращения Земли, так как по отношению к земным предметам ось гироскопа будет совершать кажущееся или видимое движение. 

Свойство прецессии состоит в том, что под действием силы, приложенной к кардановым кольцам, главная ось гироскопа перемещается в плоскости, перпендикулярной к направлению действия силы

Такое движение гироскопа называется прецессионным. Прецессионное движение будет происходить в течение всего времени действия внешней силы и прекращается с прекращением ее действия. Направление прецессионного движения определяется с помощью правила полюсов, которое формулируется следующим образом: при приложении к гироскопу момента внешней силы полюс гироскопа кратчайшим путем стремится к полюсу силы

20. Гироскопические силы. Применение гироскопов.

ГИРОСКОПИЧЕСКИЕ СИЛЫ - силы, зависящие от скоростей и обладающие тем свойством, что сумма их работ (или мощностей) при любом перемещении системы, на к-рую действуют эти силы, равна нулю.

Применение гироскопов.

• В приборе <авторулевой>

• <Автопилот>

• Инерциальная навигация

• бесплатформенные ИНС

• Системы стабилизации

21. Закон архимеда.

Закон Архимеда формулируется следующим образом: на тело, погружённое в жидкость (или газ), действует выталкивающая сила, равная весу вытесненной этим телом жидкости (или газа). Сила называется силой Архимеда:

22. Давление в жидкости и газе. Уравнение неразрывности.

p=ΔF/ΔS

23.Уравнение Бернули и следствие из его.

24. Истечение жидкости через отверстие.

25. Вязкость. Ламинарный и турбулентный режим течения.

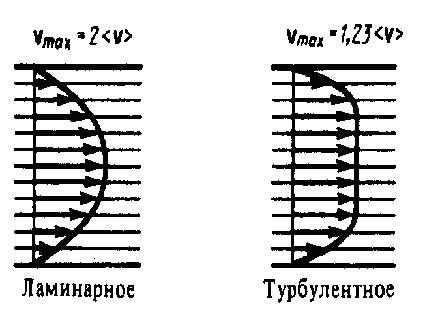Вя́зкость — одно из явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. 

26.Методы определения вязкости.

1. М 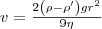етод Стокса. Этот метод определения вязкости основан на измерении скорости медленно движущихся в жидкости небольших тел сферической формы. 

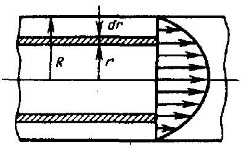2. М етод Пуазейля. Этот метод основан на ламинарном течении жидкости в тонком капилляре. Для капилляр радиусом R и длиной l в жидкости мысленно выделим цилиндрический слой радиусом r и толщиной dr

27. Движение тела в жидкости и газах.

На тело, движущееся в жидкости или газе, действуют две силы (равнодействующую их обозначим R), одна из которых (Rx) направлена в сторону, противоположную движению тела (в сторону потока), — лобовое сопротивление, а вторая (Ry) перпендикулярна этому направлению — подъемная сила

г де r — плотность среды; v — скорость движения тела; S — наибольшее поперечное сечение тела.

Лобовое сопротивление

где Су — безразмерный коэффициент подъемной силы.

Подъемная сила.