74. Спектральный анализ отклика системы: воздействие экспоненциального импульса на интегрирующую цепь.

Как пример использования спектрального метода решим задачу о прохождении экспоненциального видеоимпульса напряжения через RC-цепь. В данному случае спектральная плотность входного сигнала

и задача сводится к вычислению интеграла, входящего в выражение

.

Разлагая алгебраическую часть подынтегральной функции на элементарные дроби, имеем

.

Структура слагаемых, стоящих в квадратных скобках, позволяет непосредственно использовать результат, полученный при вычислении импульсной характеристики RC-цепи, и записать решение при t>0:

.

Естественно, что при t<0

.

75. Амплитудные модуляторы.

Модуляторы предназначены для управления одним или несколькими параметрами передаваемого колебания по закону передаваемого сообщения. Модулированное колебание имеет вид

Амплитудную модуляцию можно осуществлять как с помощью линейных, так и нелинейных преобразований. Простейшим амплитудным модулятором служит нелинейный усилитель, резонансный контур которого настроен на частоту несущего колебания.

Одна из возможных схем модуляторов и осциллограммы ее работы показаны на рисунке.

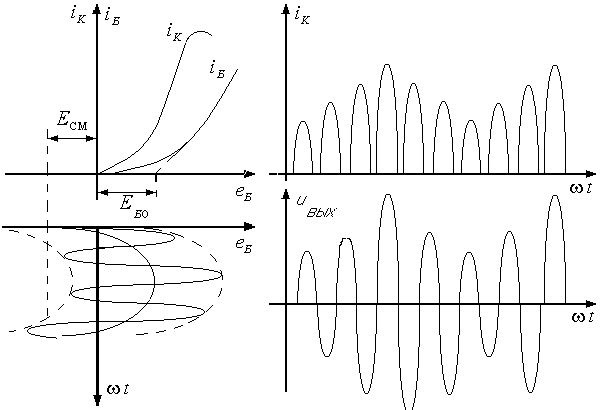
Процесс модуляции сопровождается изменением спектра модулируемого колебания и осуществляется с помощью нелинейных элементов (ламп, транзисторов). При модуляции напряжение смещения на базе изменяется в такт с модулирующим колебанием, при этом напряжение возбуждения ВЧ и коллекторное питание остаются постоянными. Режим работы усилителя выбирается нелинейным, поэтому при изменении напряжения смещения изменяется величина импульсов коллекторного тока, при этом амплитуда колебаний, выделяемых коллекторным контуром тоже будет изменяться, т.е. получаем амплитудно-модулированный сигнал.

При постоянном напряжении смещения и постоянной амплитуде возбуждающего колебания импульсы коллекторного тока имеют постоянную амплитуду и величина первой гармоники тока, также будет постоянной. Если подавать на вход транзистора только переменное напряжение НЧ управляющего сигнала, то вследствие того, что контур для колебаний НЧ имеет сопротивление близкое к нулю, в контуре колебания будут отсутствовать. При совместной подаче высокочастотного сигнала и переменного напряжения смещения изменяется величина высокочастотных импульсов коллекторного тока, в связи с этим изменяется и амплитуда тока первой гармоники сигнала, выделяемой в коллекторном контуре. Таким образом и получают АМ колебание.

76. Коэффициент передачи многокаскадных систем, логарифмическое представление коэффициента многокаскадной системы.

В случае системы с m входами и n выходами следует ввести парциальные импульсные характеристики h_ij(t), i=1,2,….; j=1,2,…., каждая из которых отображает сигнал на i-м выходе при подаче на j-й вход дельта-функции. Совокупность функций h_ij(t) образует матрицу импульсных характеристик

.

Формула интеграла Дюамеля в многомерном случае приобретает вид

, где - n-мерный вектор; - m-мерный вектор.

Частотные свойства линейной системы, имеющей m входов и n выходов, можно описать матрицей частотных коэффициентов передачи:

.

Между матрицами h(t) и K(jω) существует закон связи, аналогичный тому, который задан формулами:

.

В радиотехнике часто используют сложные системы, отдельные звенья которых включены каскадно, т.е. выходной сигнал предыдущего звена служит входным сигналом для следующего звена. Примером такой системы может служить многозвенный усилитель. Положим, что известны частотные коэффициенты передачи отдельных звеньев K_п(jω), n=1,2,…N. Возбуждая первое звено сигналом , получим на выходе сигнал , откуда результирующий коэффициент передачи

.

В инженерных расчетах АЧХ системы часто выражают в логарифмических единицах – децибелах. Если на некоторой частоте w известен модуль частотного коэффициента передачи, то усиление системы, выраженное в децибелах (дБ), . Если <1, то система ослабляет сигнал и усиление оказывается отрицательным. Легко видеть, что при каскадном соединении звеньев их усиления суммируются автоматически: .