14. Основные свойства преобразования фурье.

Линейность преобразования Фурье.

Если некоторый радиосигнал f(t) образуется как взвешенная сума некоторой совокупности исходных сигналов, то спектральная плотность такого сигнала может быть определена через спектральную плотность составляющих компонент:

(7.1)

r_i – постоянный весовой коэффициент, F_i() – спектральная плотность одного из сигналов, входящих в совокупность. Справедливость этой формулы легко проверить непосредственной подстановкой.

Спектральная плотность сигнала, смещенного во времени.

Допустим . Нужно найти изображение сигнала смещенного во времени f(t-t₀). Можно показать, что сигнал f(t-t₀) имеет спектральную плотность (7.2)

Комплексное число exp(-jt₀) при любых t₀ имеет модуль 1. Поэтому амплитуды элементарных гармоник, из которых складывается сигнал не зависит от его смещения вдоль оси времени, а информация о его смещении заключена в фазовом угле его спектра.

Спектральная плотность производной и интеграла.

Допустим задан сигнал f(t) и его спектральная плотность F(), а нужно найти спектр производной:

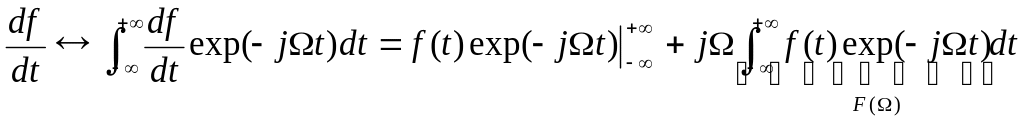(7.3)

(7.4)

Пи дифференцировании, как видно из формулы, скорость изменения сигнала во времени возрастает в  раз, отсюда следует, что в области высоких частот вес спектральных компонент возрастает по сравнению со спектром исходного сигнала. Можно показать, сто при многократном дифференцировании спектр сигнала вычисляется: (7.5)

Т. о. дифференцирование сигнала во времени эквивалентно алгебраической операции умножения на j в спектральной области  говорят, что оператор j является оператором дифференцирования в частотной области.

Спектр от интеграла функции.

(7.6)

Рис. 7.1

В РТ - устройствах часто формируют сигнал с помощью операции интегрирования (7.6) на схемах устройство интегрирования выглядит также как на рис. 7.1.

Можно показать, что в этом случае спектральная плотность проинтегрированного сигнала может быть определена по спектральной плотности исходного сигнала:

(7.8)

При многократном интегрировании: (7.9)

Т. о. оператор j и связанный м ним множитель 1/ j выступает как оператор интегрирования в области спектра.

15. Спектральная плотность произведения сигналов и неинтегрируемых импульсов.

Если заданы две функции f₁(t) и f₂(t), определенные на интервале -<t<+, то новую функцию называют сверткой двух функций f₁(t) и f₂(t) и символически ее обозначают и читают: функция f₁(t) свернута с функцией f₂(t). .

Свертка обладает известными в линейной алгебре свойствами коммутативности, ассоциативности и дистрибутивности. Если функции и , то спектральная плотность свертки:

.

Используя формулу прямого преобразования Фурье:

Введя новую переменную : .

Поскольку и , то т. о. действительно приходим к выражению (7.12). Т. о. если известны спектры функций входящих в свертку, то спектр свертки определяется как произведение спектров функций свертки.

Можно так же показать, что спектр произведения двух функций может быть найден как свертка спектров функций входящих в произведение: (7.13)

Причем под сверткой спектров понимается выражение: .

Интеграл в правой части и называется сверткой спектров. Т. о. показано то, что спектральная характеристика свертки равна произведению спектральных плотностей свертываемых функций, а свертка спектральных плотностей равна спектральной плотности произведения функций.

Спектральная плотность неинтегрируемых сигналов.

а) Спектральная плотность постоянного в интервале -<t<+ сигнала.

Допустим, что такой сигнал имеет неизвестную пока спектральную плотность F()  очевидно, что должно быть справедливо обратное преобразование Фурье: . Учитывая фильтрующие свойства  - функции: (7.16)

Т. о., постоянный во времени сигнал имеет постоянную компоненту только на нулевой частоте.

б) Спектральная плотность комплексного экспоненциального сигнала.

Допустим, что экспоненциальный сигнал задан в виде . Будем считать, что этот сигнал имеет некоторую спектральную плотность F(), тогда: (7.17)

Последнее равенство верно только, если: (7.18)

Т. е. спектральная плотность этого сигнала равна нулю всюду, кроме точки ₀, где она равна  - функции.

в) Спектральная плотность гармонических колебаний.

Допустим, что исходный сигнал или . Используя формулу Эйлера можно записать: и .

Используя выражение для спектральной плотности экспоненциального сигнала (7.18) можно записать:

(7.20)

г) Спектральная плотность прямоугольного радиоимпульса.

Радиоимпульс аналитически может быть записан в виде: (7.21)

Причем спектр огибающей (видеосигнала) будем считать известным и равным , а спектр косинусоидального импульса: (7.22)

Спектр радиоимпульса представляет собой свертку спектров двух сигналов. Используя формулу свертки и учитывая фильтрующие свойства  - функции можно найти, что спектр радиоимпульса будет иметь вид:

.