12. Интеграл фурье.

Для разложения функций в ряд Фурье функции должны быть периодическими. Однако многие физически реализуемые сигналы нельзя считать периодическими. Для анализа таких сигналов используют более общие представления сигналов с помощью интеграла Фурье.

Пусть задан одиночный импульсный сигнал 1 (см. рис.) с конечной энергией. Чтобы к такому сигналу можно было применить математический аппарат рядов Фурье, дополним одиночный сигнал 1 последовательностью таких же сигналов отстоящих на время Т.

О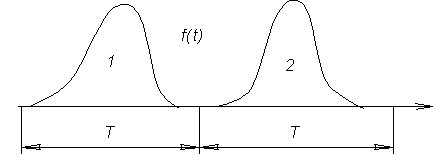 днако чтобы считать сигнал одиночным будем предполагать, что период . Формально такой сигнал можно представить в виде ряда Фурье например в форме:

, (3.8)

где 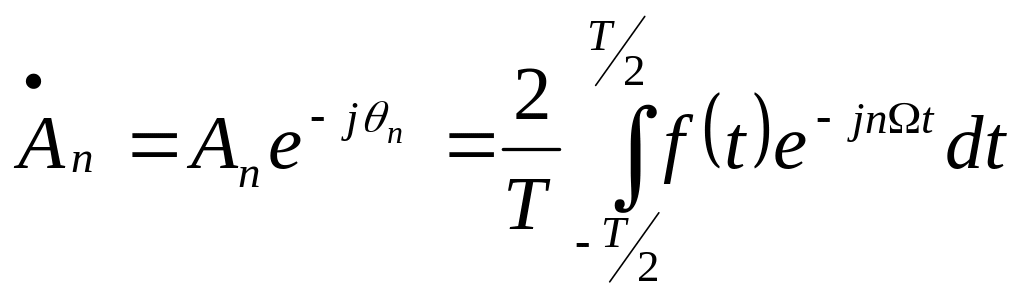. (3.9)

Подставляя в (3.8) запишем .

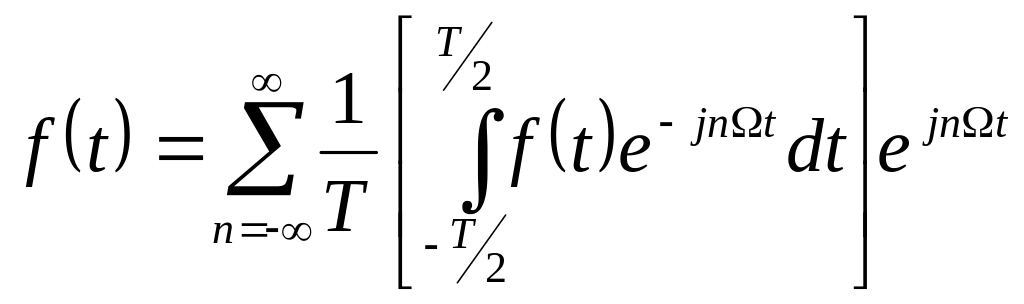Заменим , тогда (4.1)

При основная частота (характеризующая расстояние между соседними гармоническими составляющими в спектре) превращается в и величину можно рассматривать как текущую частоту . Операцию суммирования в выражении (4.1) можно заменить операцией интегрирования. Таким образом, приходим к двойному интегралу вида (4.2)

Внутренний интеграл в формуле (4.2) (4.3)

зависящий от текущей частоты , называют спектральной плотностью или спектральной характеристикой сигнала. С учетом обозначения спектральной плотности получаем (4.4)

Формулу (4.3) называют прямым, а формулу (4.4) обратным преобразованием Фурье.

Сравнение формул (3.9) и (4.3) показывает ( )

(3.9) (4.3), что , или учитывая, что получим . (4.5)

Таким образом, получается как результат деления амплитуды n-ой гармоники на полосу частот определяющую соседние линии дискретного спектра, т.е. имеет смысл плотности амплитуд и имеет размерность .

Спектр непериодического сигнала сплошной, поскольку при соседние спектральные линии располагаются как угодно близко друг к другу.

Из совпадения выражений (3.9) и (4.3) вытекает следующее важное положение: Огибающая сплошного спектра (модуль спектральной плотности) непериодической функции и огибающая линейчатого спектра периодической функции (полученной из непериодической путем продолжения ее с периодом Т) совпадают по форме и отличаются только масштабом. Спектральная плотность обладает всеми свойствами амплитуд гармоник.

13. Примеры определения спектральной плотности.

а) Спектральная плотность сигналов прямоугольного видеоимпульса.

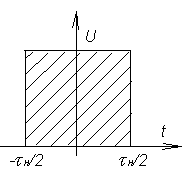Рис.4.2 Рис.4.3

П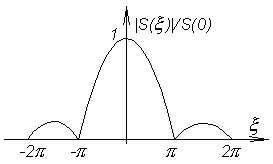 усть сигнал имеет амплитуду и длительность . Найдем по формуле (4.3) спектральную плотность.

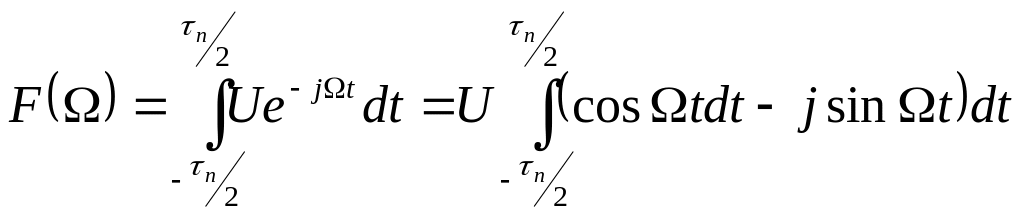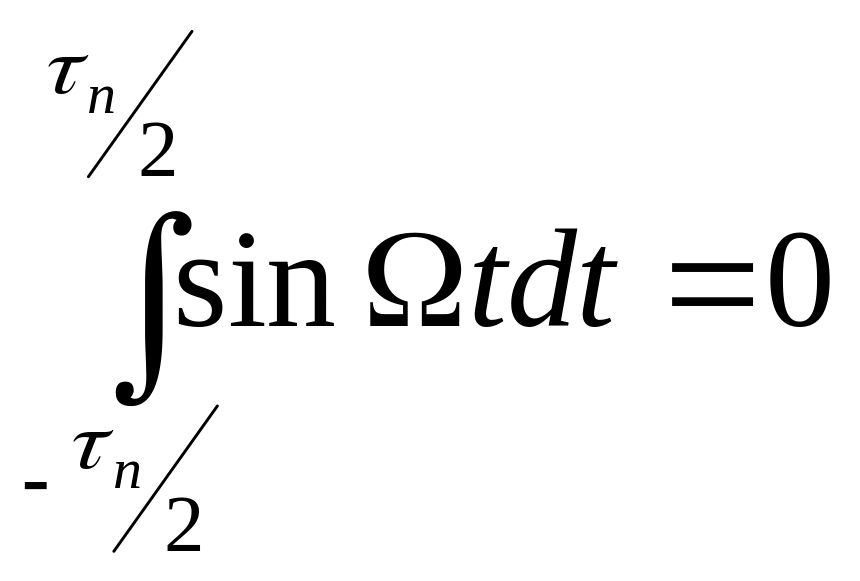, т.е.

Введя безразмерную переменную выражение для спектральной плотности запишем в виде

(4.6)

график функции показан на рис 4.3.

б) Спектральная плотность экспоненциального видеоимпульса.

Р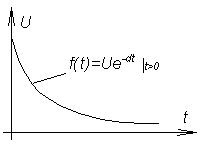 ис.4.4 Рис.4.5

И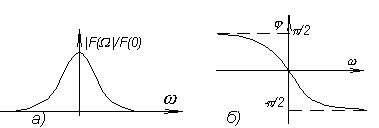 мпульс задан на рис.4.4. Найдем .

(4.7)

как видно из формулы (4.7) является комплексной функцией. Модуль , аргумент . Показаны на рис 4.5.

в) Спектральная плотность -импульса.

Пусть сигнал f(t) представляет собой -импульс, сосредоточенный в т. t=0 и имеющий плотность A:

.

Спектральная плотность сигнала м.б. определена по известной формуле:

, t=0 (4.8)

Данный интеграл будет равен значению подынтегральной функции в т. t=0, где локализован -импульс: exp(0)=1. Следовательно F()=A=const.

Т.о., -импульс имеет равномерный спектр на всех частотах. Возникновение бесконечно большого по амплитуде импульса в момент t=0 можно рассмотреть как результат совпадения по фазе бесконечно большого числа суммируемых гармоник, из которых слагается -импульс. В другие моменты времени из-за несимфазности гармоник результирующий сигнал получается равным нулю.

Связь между длительностью импульса и шириной его спектра.

Под шириной спектра сигнала обычно понимают интервал частот, в пределах которого модуль спектральной плотности не меньше некоторого наперед заданного уровня (напр. 0.1 F_maxF_max).

Рассмотрим прямоугольный видеоимпульс, для которого за верхнюю частоту спектра примем частоту, соответствующую первому нулю спектральной плотности. Эту частоту можно найти из условия:

(4.9)

В случае экспоненциального видеоимпульса условимся, что на граничной верхней частоте модуль спектральной плотности уменьшается в 10 раз по сравнению с максимальным значением  (4.10)

Эффективная длительность импульса также определяется из условия:

(4.11)

Для -импульса, имеющего бесконечно малую длительность спектр неограниченно протяжен вдоль оси частот. Из рассмотрения этих трех сигналов можно сделать вывод: чем меньше длительность импульса, тем шире его спектр. Произведение ширины спектра на его длительность есть постоянное число, которое зависит только от формы импульса: (4.12)

Min значение имеет место для колокольного (гауссова) импульса: .

Такую форму обычно приобретает огибающая прямоугольного радиоимпульса. Прошедшего через большое число резонансных каскадов в приемнике. Формула (4.12) имеет большое значение для РТ, т.к. позволяет определить требования к полосе пропускания РТ-го устройства при заданной длительности импульса. Из рассмотренного следует, что чем короче сигнал и его форма, тем шире полоса пропускания устройства. Короткие импульсные помехи, обладающие широким спектром, могут ухудшать условия приема в широкой полосе частот.