10. Разложение периодических сигналов на гармонические составляющие. Ряд фурье.

Для анализа радиотехнических устройств хорошо разработаны методы, основанные на применении гармонических сигналов. Для сигналов сложной формы использование методов расчета и анализа цепей при гармонических воздействиях допустимо, если представить сложный сигнал в виде совокупности гармоник. Из математики известно, что периодические функции, удовлетворяющие условиям Дирихле можно представлять в виде тригонометрических рядов. Функция Дирихле сводится к требованиям, чтобы функция имела в интервале конечное число экстремальных точек и конечных разрывов (разрывов первого рода). Согласно теории Фурье функция f(x) с периодом 2 может быть разложена в тригонометрический ряд:

(3.2.1)

Коэффициенты a₀, a₁, ... a_n и b₁, b₂, ... b_n, называемые коэффициентами Фурье, определяются выражениями 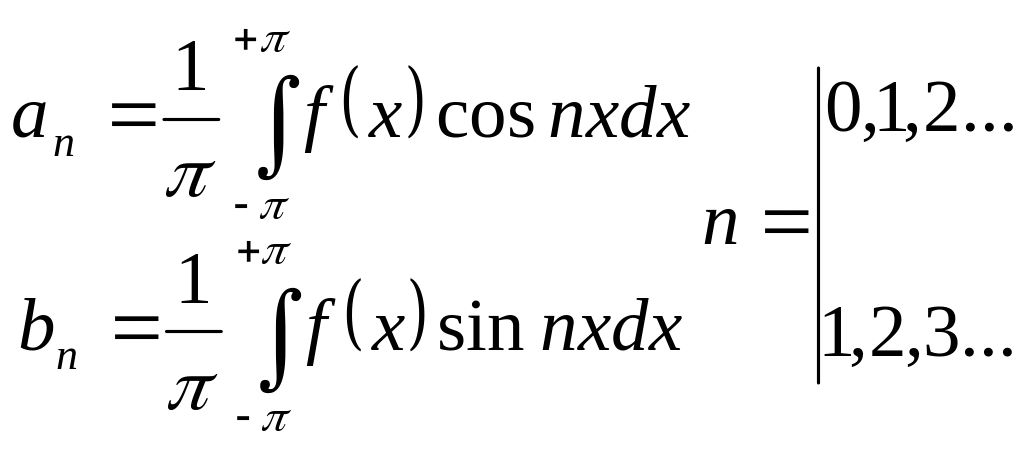(3.2.2)

Для физических процессов протекающих во времени в качестве аргумента выступает время, т. е.t. Кроме того сумма синусоидальной и косинусоидальной составляющих могут быть представлены в виде результирующих гармоник, т. е. (3.2.3), где и .

Таким образом функция f(t) представляется в формуле: (3.2.4)

Совокупность гармонических составляющих, на которые раскладывается функция f(t) называется спектром сигнала (функции). Из формулы (3_2.4) следует, что спектр гармонической функции состоит из постоянной составляющей и множества гармоник, с частотами образующими дискретный ряд значений .

Графическое и комплексное представление спектров.

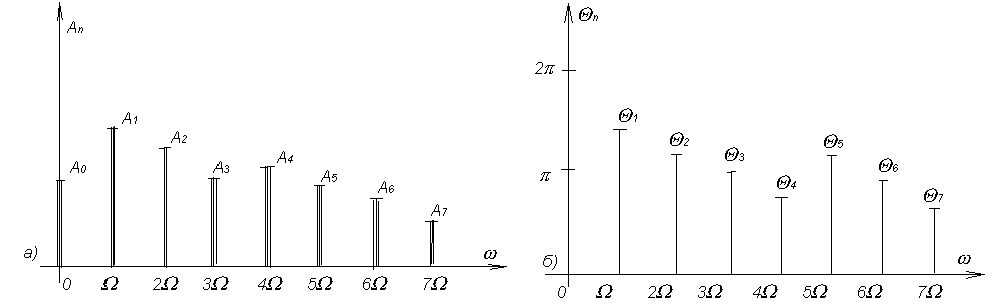
Рис. 3.2.1 - Графическое представление линейного спектра.

Спектр функции может быть изображён графически. На рисунке 3.2.1 показаны спектральные диаграммы некоторого произвольного сигнала. Рис. 3.2.1а) называют амплитудной диаграммой спектра или амплитудным спектром, рис. 3.2.1б) называют фазовой диаграммой или фазовым спектром. На рис. 3.2.1а) отложены по вертикали отрезки имеющие длину равную А_n - амплитуде соответствующей гармоники, а на рис. 3.2.1б) значение начальных фаз гармоник.

11.Спектры простейших периодических функций.

Р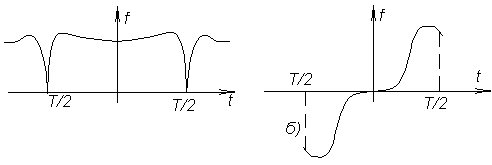 яды Фурье для чётных и нечётных функций. Пусть функция f(t) чётная (симметричная относительно оси ординат рис.а)), т.е. .

Разложение функции будет следующим

,(2)

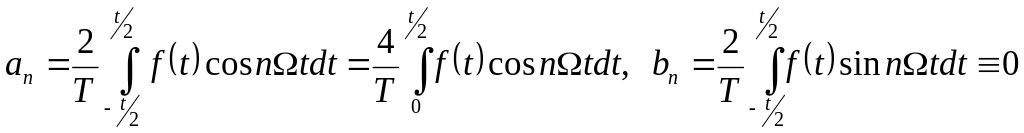где . (1)

Аналогично для нечётной функции можно найти, что (3.2.12)

Спектр последовательности прямоугольных импульсов.

Н а рисунке 3.2.3 показана последовательность прямоугольных импульсов, которую можно рассматривать как чётную функцию. По формуле (1) находим амплитуду n-ой гармоники:

.

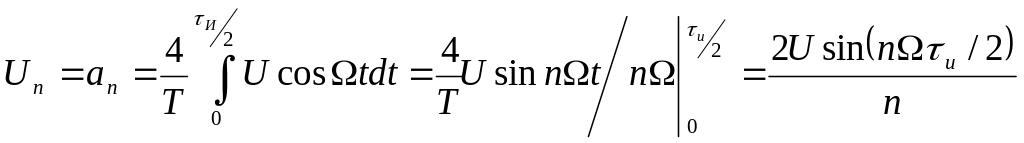Пост. сост-щая напряж-я равна: 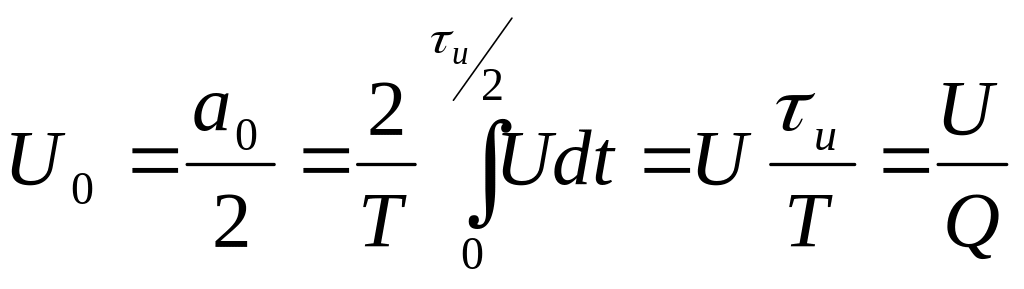; ,где Q - скважность импульсов.

Разложение функции запишется в виде: . (3.2.15)

В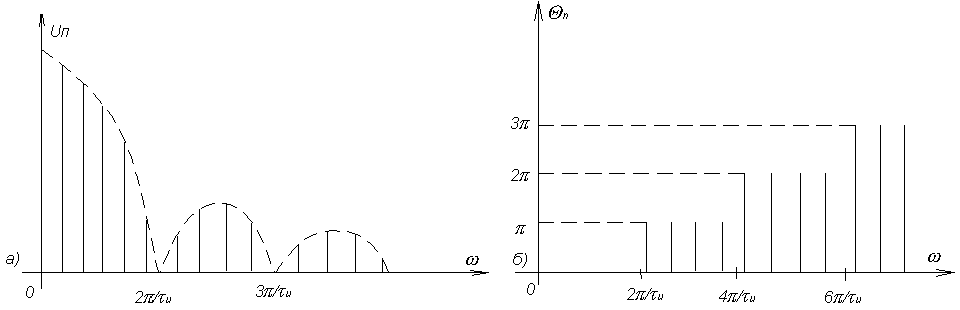 общем случае спектр прямоугольных импульсов может быть изображён как показано на рис. 3.2.4 а) и б). Расстояние между отдельными спектрами составляющими обратно пропорционально периоду следования импульсов - Т, а положение нулей кратно .

Мощность и действующее значение переменного периодического тока.

Пусть несинусоидальный периодический ток i(t) течёт через активное сопротивление r. Средняя за период мощность будет равна: . Здесь p(t) - мгновенная мощность.

Представим функцию i(t) в виде ряда Фурье, тогда

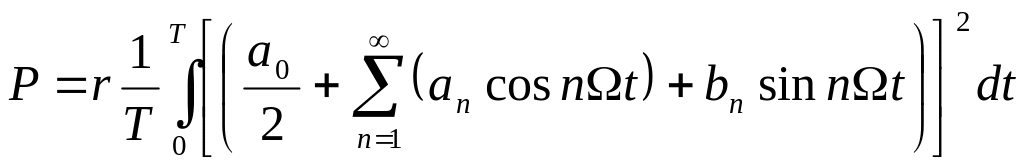
Поэтому после интегрирования получим: ,

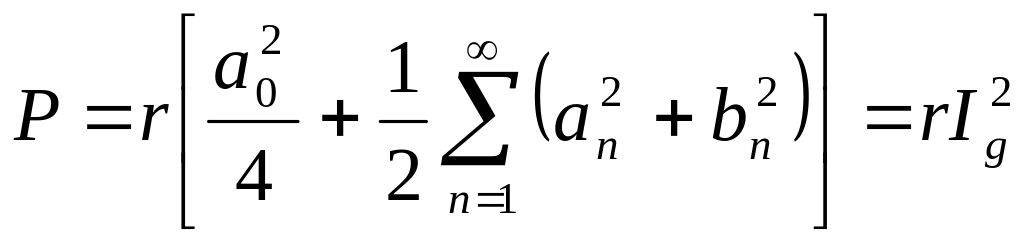где ; ; ; .

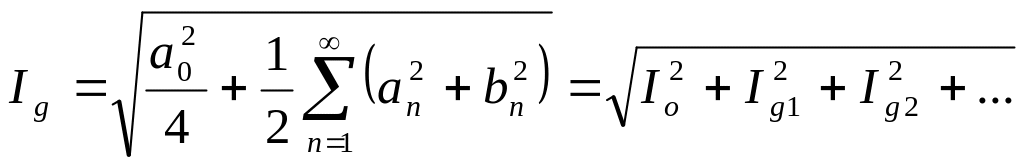Величины I_g, I₀, I_g1, I_g2, ... называют действующими значениями тока. Аналогично вычисляется и действующее значение напряжения.

Если сопротивление r=1 Ом, то мощность равна: .

В таком виде это соотношение носит название равенство Парсеваля.