8. Скалярное произведение сигналов и его свойства.

В обычном трехмерном пространстве два вектора и имеют квадрат модуля определяемый соотношением: , (4.9.) где - скалярное произведение этих двух векторов, зависящее от угла между ними.

Запишем выражение для энергии суммы двух сигналов: (4.10.) В отличии от самих сигналов их энергии не аддитивны т. е. энергия суммарного сигнала дополнительно содержит взаимную энергию (4.11.), которая как это следует из сравнения структур формул (4.9.) и (4.10.) аналогично скалярному произведению . Поэтому скалярное произведение двух сигналов (4.12.) (4.13.)

Скалярное произведение обладает следующими свойствами:

1. ; 2. (4.14.); 3. , где  - число; 4.

Линейное пространство, в котором введено скалярное произведение (4.12.) и выполняются условия (4.14.) называется вещественным Гильбертовым пространством (). В математике показано, что в  - пространстве выполняется неравенство Коши - Буняковского: (4.15.)

Если сигналы являются комплексными величинами, то говорят о комплексном  - пространстве в котором скалярное произведение задается соотношением: (4.16.)

9. Ортогональные системы и обобщенные ряды фурье.

Два сигнала U и V называются ортогональными, если их скалярное произведение, а значит и взаимная энергия равны нулю: .

Допустим в  - пространстве задана система функций попарно ортогональных на временном интервале t₁ t₂ и обладающих единичными нормами:

В этом случае говорят, что в пространстве сигналов задан ортонормированный базис. Разложим произвольный сигнал S(t)  в ряд: . (1) Представление сигнала ряда (1) называется обобщенным рядом Фурье для сигнала S(t) в выбранном базисе. Коэффициенты этого ряда находят обычно следующим образом. Выберем базисную функцию U_K с номером K и умножим на ее обе части равенства, а затем проинтегрируем полученное произведение в заданном интервале t₁ t₂ тогда получим:

Ввиду ортонормированности выбранного базиса в первой части выражения не равно 0 только одно слагаемое для которого i=K, поэтому получим: (2)

Использование обобщенного ряда Фурье позволяет при изучении сигналов перейти от бесконечного числа значений сигналов и рассмотрению коэффициента обобщенного ряда Фурье. Если сигнал задан обобщенным рядом Фурье , то его энергия может быть вычислена:

Которые в следствии ортонормированности приводят к виду: , т. е. энергия сигнала равна сумме энергий всех компонентов из которых складывается обобщенный ряд Фурье.

Оптимальность разложения сигнала по ортогональному базису.

Для сигнала S(t) введем конечномерную аппроксимацию: с неизвестными коэффициентами C_k и потребуем, чтобы эти коэффициенты удовлетворяли условию минимальной энергии ошибки аппроксимации, т. е. условию:

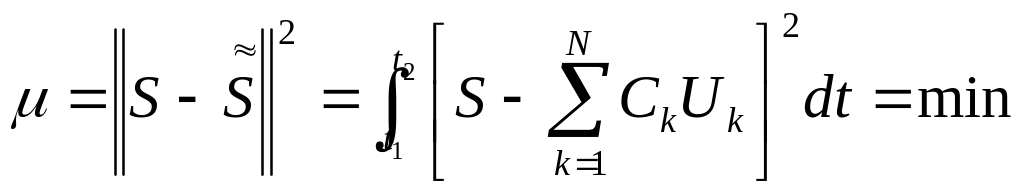
Необходимое условие min состоит в том, что C_k должны удовлетворять условию системы:

k=1…N (3) В развернутом виде ошибка аппроксимации которую необходимо дифференцировать по C­_k имеет вид:

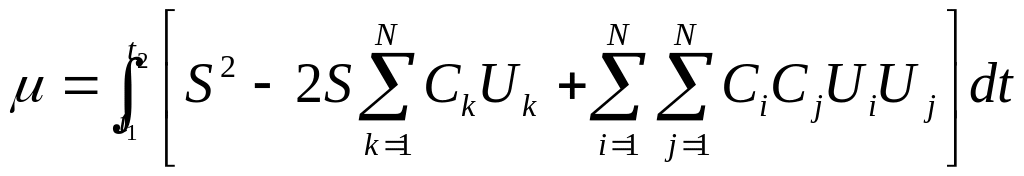
Поскольку использованная базисная система функции ортогональна и кроме того все слагаемые не содержащие коэффициент C_k дают равные нули производные, то можем записать:

или

Учитывая, что базисная функция имеет единичную норму, получим, что система уравнений (3) с учетом последней записи может быть представлена в виде: имеет

Т. о., получим, сто формула вычисления коэффициента C_k удовлетворяющая условию минимума ошибки аппроксимации совпадают с формулой (2) для вычисления коэффициента обобщенного ряда Фурье. Таким образом, использование ограниченного по длине ряда Фурье с ортогональными функциями, обеспечивает экстремальное значение ошибки аппроксимации, а вычисляя вторую производную для энергии ошибок аппроксимации можно было бы показать, что разложение в обобщенный ряд Фурье обеспечивает не просто экстремум, а именно минимальное значение ошибки аппроксимации.