4. Функция включения и дельта-функция.
Функция включения. Допустим, математическая модель сигнала задана в виде:
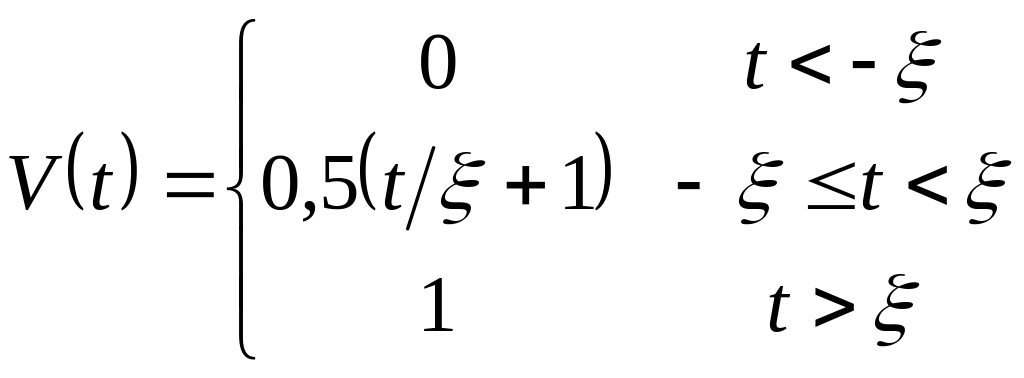
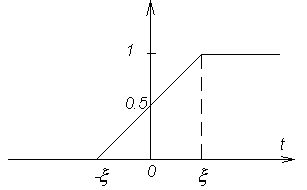(3.1.2)
Эта функция
описывает процесс перехода некоторого
физического объекта из нулевого в
единичное состояние. Переход совершается
по линейному закону за время
.
Если
стремится к нулю, то в пределе переход
из одного состояния в другое будет
происходить мгновенно.
Математическую
модель этого предельного сигнала
называют функцией включения или функцией
Хевисайда. Она получила спец. название
и обозначение
или
.
Аналитически единичный скачок можно записывать в виде:
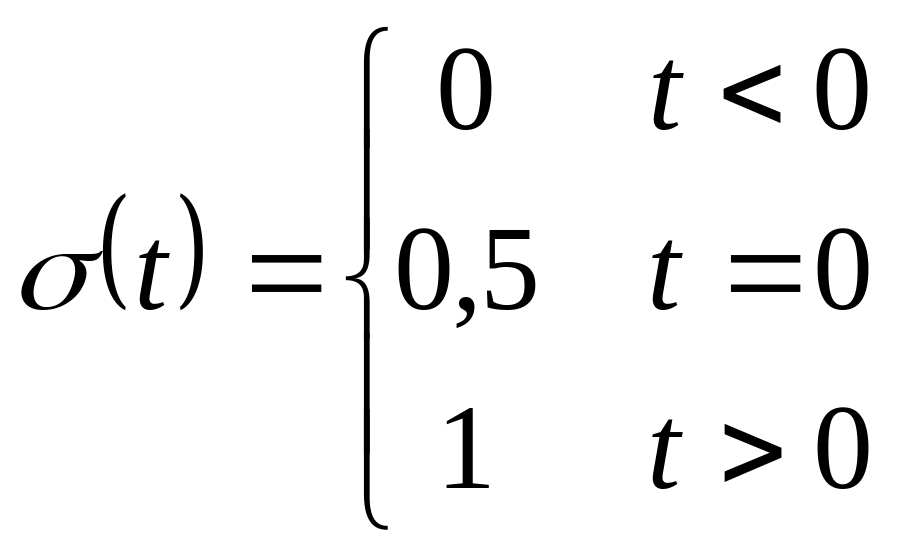или для смещенной
относительно начала координат функции: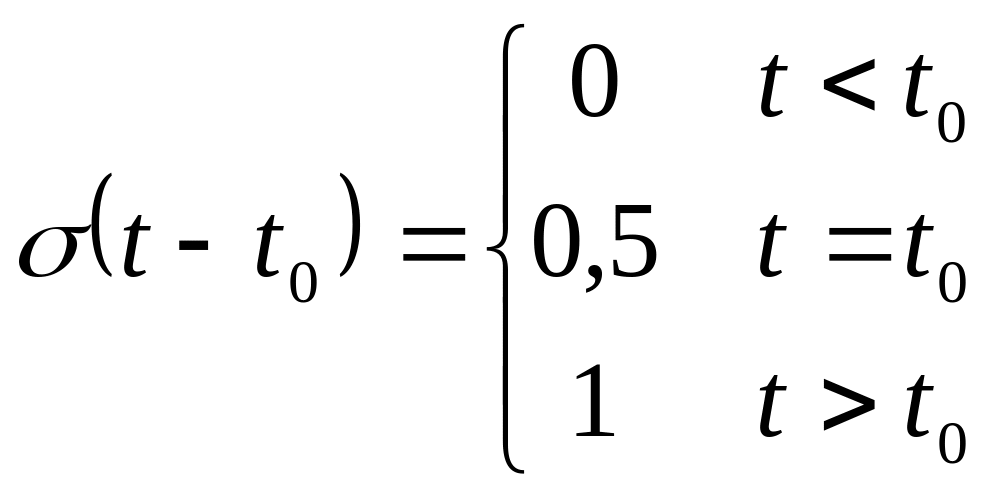
Возможны и другие аналитические формы
записи единичной функции. С помощью
функции включения можно описать любую
произвольного вида функцию. Для функции
показанной на рисунке 3.1.3 получим
(3.1.4)
Е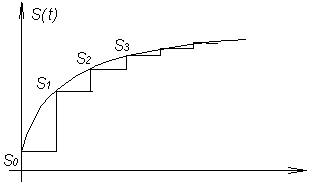
сли
в полученном выражении шаг
устремить к нулю, то дискретную переменную
k
можно заменить непрерывной переменной
. Малые приращения
превратится в дифференциалы
и можно прийти к интегральной форме
динамического представления произвольного
сигнала:
(3_1.5)
Дельта-функция. При втором способе динамического представления сигналов используется понятие дельта-функции. Рассмотрим импульсный прямоугольный сигнал, заданный в виде двух функций включения:
(3_1.6)
П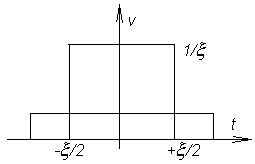
лощадь
этого импульса при любом значении
параметра равна
1. Например, если -
напряжение, то
.
Если величина
стремится к нулю, то импульс, сокращаясь
по длительности, сохраняет свою площадь,
поэтому его высота неограниченно
возрастает. Предельное значение такой
функции при
носит название дельта-функции или
функции Дирака и обозначается
(3.1.7)
Дельта-функция
равна нулю всюду за исключением точки
(говорят, что функция
сосредоточена в этой точке). Несмотря
на то, что функция
сосредоточена в точке, она обладает
единичным интегралом:
.
Н а рисунке 3.1.5 показано символическое обозначение функции . Свойства дельта-функций присущи некоторым обычным функциям при их предельном представлении. Примером служат следующие две функции:
;
5. Динамическое представление произвольного сигнала с помощью дельта-функции.
Обратимся снова
к рисунку 3.1.1(б) на котором сигнал
представлен совокупностью примыкающих
друг к другу прямоугольных импульсов.
Если
- значение сигнала на k-том
отсчете, то элементарный импульс с
номером k представляется
в виде:
(3.1.9)
При динамическом
представлении исходный сигнал
должен рассматриваться как сумма
элементарных импульсов:
(3.1.10)
В этой сумме при
любом дискретном значении t отличается
от нуля только одно слагаемое с номером
k, для которого
Если представить
полученную сумму в виде:
(3.1.11)
при
получим в пределе
и следовательно
(3.1.12)
Из формулы (3_1.6) и определения дельта - функции следует, что она имеет размерность частоты. Из формулы (3_1.12) видно, что если непрерывную функцию умножить на дельта - функцию и произведение проинтегрировать по времени, то в результате получим мгновенное значение функции в точке t, где сосредоточен -импульс. Отсюда вытекает и структурная схема для измерения мгновенных значений сигнала . Схема состоит из перемножителя и интегратора. Изменение в этой схеме будет тем точнее чем короче будет реальный видеоимпульс, приближенно имитирующий дельта - функцию. На основании соотношения (3.1.12) и схемы 3.1.6 говорят, что дельта-функция обладает фильтрующими свойствами.