30. Метод инвариантных частотных характеристик.
Создать ЦФ, частотная
характеристика которого в точности
повторяла бы частотную характеристику
аналоговой цепи принципиально невозможно.
Причиной этого является периодичность
частотного коэффициента передачи ЦФ,
с периодом, определяемым шагом
дискретизации
.
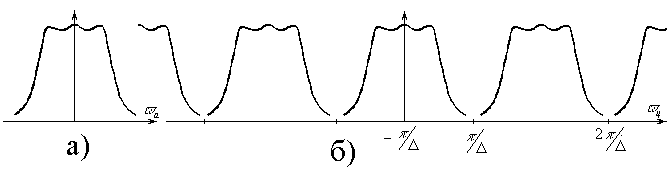
Если задана
частотная характеристика аналогового
фильтра рис.а, то от ЦФ можно требовать
только, чтобы в диапазоне
сохранялся общий вид частотной
характеристики.
Между оператором
передаточной функции аналогового
фильтра
,
задаваемой обычно в виде дробно-рациональной
функции и оператором
существует связь:
или
(21.14)
которую трудно
представить однозначно с помощью
дробно-рациональной функции от
.
В качестве некоторого приближения к
функции (21.14) служит связь вида
.
(21.15а)
Для этой связи
сделав подстановку
получим
;
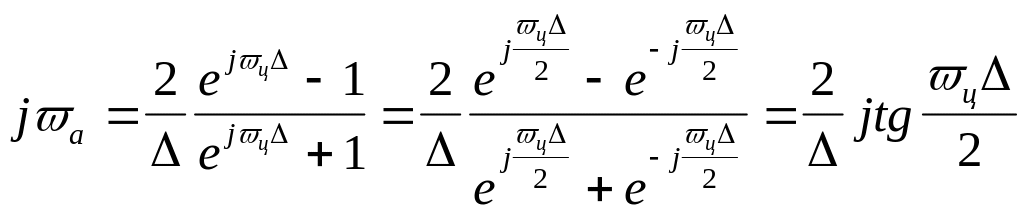(21.15б)
При достаточно
большой частоте дискретизации
и, следовательно,
.
Поэтому практическая процедура синтеза
по инвариантным частотным характеристикам
аналоговой цепи производиться заменой
переменной в функции
по формуле (21.15а). Полученная при этом
система функции ЦФ оказывается
дробно-рациональной и позволяет
непосредственно записать алгоритм
цифровой фильтрации.
Пример:
Рассмотрим ФНЧ, для которого аналоговый
прототип имеет частотную характеристику,
выражаемую в форме:
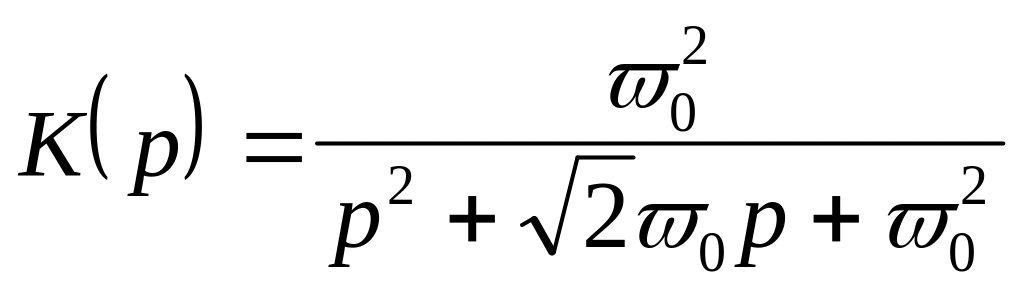(21.16)
Будем считать
заданную частоту среза ЦФ
и частоту дискретизации
.
При этих условиях шаг дискретизации
и частота среза аналогового фильтра по
формуле (21.15) получается равной:
(21.17)
Производя замену оператора в выражении (21.16) на основе соотношения (21.15а) найдем
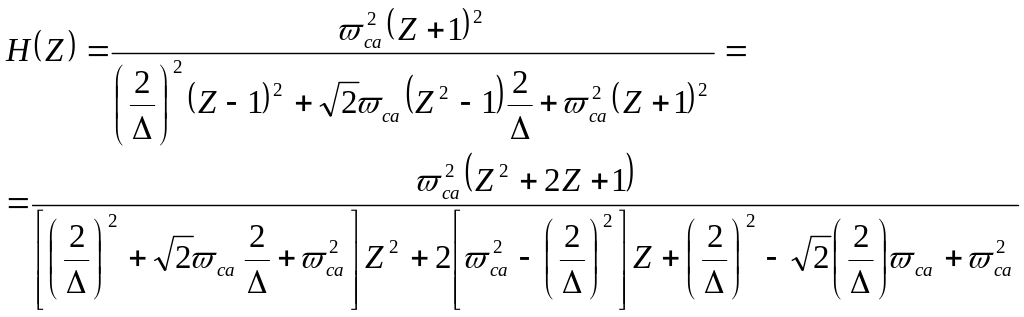(21.18)
Подставляя числовые
значения
и
можно прийти к следующему результату
(21.19)
Таким образом синтезирован ЦФ по его аналоговому прототипу, заданному частотными характеристиками.
С одержание к первой пачке.
1. Понятие сигнала. 1
2. Гармонический сигнал. 2
3. Понятие многомерного сигнала. Динамическое представление сложных сигналов. 3
4. Функция включения и дельта-функция. 4
5. Динамическое представление произвольного сигнала с помощью дельта-функции 5
6. Геометрические методы в теории сигналов. 6
7. Понятие координатного базиса линейного пространства. 7
8. Скалярное произведение сигналов и его свойства. 8
9. Ортогональные системы и обобщенные ряды Фурье. 9
10. Разложение периодических сигналов на гармонические составляющие. Ряд Фурье. 10
11.Спектры простейших периодических функций. 11
12. Интеграл Фурье. 12
13. Примеры определения спектральной плотности. 13
14. Основные свойства преобразования Фурье. 15
15. Спектральная плотность произведения сигналов и неинтегрируемых импульсов. 16
16. Основные определения и понятия в теории преобразования Лапласа. 17
17. Основные свойства преобразования Лапласа. 18
18. Взаимная спектральная плотность сигналов. Энергетический спектр. 19
19. Функция автокорреляции сигнала. 21
20. Функция автокорреляции неограниченно протяженного гармонического сигнала. 22
21. Операторный метод анализа систем. Пример анализа интегрирующей RC-цепи
операторным методом при воздействии скачка и прямоугольного импульса. 23
22. Разновидности частотно-избирательных цепей и их частотные характеристики:
последовательный и параллельный связный контуры 24
23. Функция автокорреляции дискретных сигналов. 25
24. Амплитудная модуляция – основные понятия. 26
25. Принцип амплитудной модуляции. 27
27. Алгоритмы дискретного преобразования Фурье. 29
29. Согласованная фильтрация комплекснозначных сигналов. 30
30. Метод инвариантных частотных характеристик. 31