23. Функция автокорреляции дискретных сигналов.
Используя различные
способы кодирования сигналов возможно
представить любой сигнал как совокупность
трех значений (0, 1).
Понимая под каждым из этих значений
определенную величину (амплитуды, фазы
или любого другого параметра). Для таких
дискретных сигналов применяемы понятия
функции корреляции и функции взаимной
корреляции. И в этом случае выражения
для корреляционной функции могут
записываться в следующем виде:
(10.17)
И функция
автокорреляции будет иметь вид:
(10.18)
Физический смысл этих величин может быть определен как взаимная энергия сигналов.
Пример дискретной функции автокорреляции.
Рассмотрим часто применяемый в РЛ сигнал называемый семипозиционным кодом Бартера.
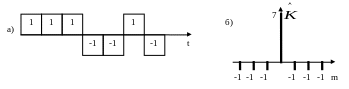
Рис. 10.4
По заданному сигналу заполним таблицу.
1 |
1 |
1 |
-1 |
-1 |
1 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
-1 |
-1 |
1 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
-1 |
-1 |
1 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
-1 |
-1 |
1 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
-1 |
-1 |
1 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
-1 |
-1 |
1 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
-1 |
-1 |
1 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
-1 |
-1 |
1 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
-1 |
-1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
-1 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
Сигнал и его код и сдвинутые его копии, а так же функция автокорреляции показаны на рис. 10.4 а, б. Функция автокорреляции сигнала имеет значительный максимум при нулевом сдвиге и благодаря этому может быть обеспечено хорошее выделение такого сигнала на фоне помех.