
- •1. Понятие сигнала.
- •2. Гармонический сигнал.
- •3. Понятие многомерного сигнала. Динамическое представление сложных сигналов.
- •Динамическое представление сложных сигналов
- •4. Функция включения и дельта-функция.
- •Н а рисунке 3.1.5 показано символическое обозначение функции . Свойства дельта-функций присущи некоторым обычным функциям при их предельном представлении. Примером служат следующие две функции:
- •5. Динамическое представление произвольного сигнала с помощью дельта-функции.
- •6. Геометрические методы в теории сигналов.
- •7. Понятие координатного базиса линейного пространства.
- •8. Скалярное произведение сигналов и его свойства.
- •9. Ортогональные системы и обобщенные ряды фурье.
- •10. Разложение периодических сигналов на гармонические составляющие. Ряд фурье.
- •11.Спектры простейших периодических функций.
- •12. Интеграл фурье.
- •13. Примеры определения спектральной плотности.
- •14. Основные свойства преобразования фурье.
- •15. Спектральная плотность произведения сигналов и неинтегрируемых импульсов.
- •16. Основные определения и понятия в теории преобразования лапласа.
- •Б ) Найдем изображение экспоненциального сигнала ,
- •17. Основные свойства преобразования лапласа.
- •18. Взаимная спектральная плотность сигналов. Энергетический спектр.
- •19. Функция автокорреляции сигнала.
- •20. Функция автокорреляции неограниченно протяженного гармонического сигнала.
- •21. Операторный метод анализа систем. Пример анализа интегрирующей rc-цепи операторным методом при воздействии скачка и прямоугольного импульса.
- •22. Разновидности частотно-избирательных цепей и их частотные характеристики: последовательный и параллельный связный контуры.
- •23. Функция автокорреляции дискретных сигналов.
- •24. Амплитудная модуляция – основные понятия.
- •25. Принцип амплитудной модуляции.
- •27. Алгоритмы дискретного преобразования фурье.
- •29. Согласованная фильтрация комплекснозначных сигналов.
- •30. Метод инвариантных частотных характеристик.
- •С одержание к первой пачке.
- •1. Понятие сигнала. 1
- •5. Динамическое представление произвольного сигнала с помощью дельта-функции 5
21. Операторный метод анализа систем. Пример анализа интегрирующей rc-цепи операторным методом при воздействии скачка и прямоугольного импульса.
Операторный метод анализа систем базируется на представлении входных и выходных сигналов их преобразованиями Лапласа.
Решение дифференциальных уравнений операторным методом. Преобразование Лапласа явл-ся исключительно гибким и мощным методом, позволяющим путем стандартных процедур находить решения линейных диф. уравнений с постоянными коэффициентами. Именно это свойство обусловило его широкое применение в научных исследованиях и инженерных расчетах.
Пусть диф. уравнение
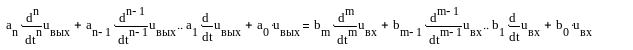
устанавливает закон соответствия между сигналами на входе и выходе некоторой линейной стационарной системы. Примем, что область допустимых входных сигналов не содержит в себе функций, столь быстро нарастающих во времени, что для них не существует преобразования Лапласа.
Обозначим закон соответствия между оригиналами и изображениями следующим образом:
![]() .
Вычислив преобразование Лапласа от
обоих частей уравнения, получим:
.
Вычислив преобразование Лапласа от
обоих частей уравнения, получим:
![]()
Важнейшей
характеристикой, на которой основан
операторный метод, является отношение
изображений выходного и входного
сигналов:
![]() ,
называемое передаточной функцией
или операторным коэффициентом
передачи рассматриваемой системы.
,
называемое передаточной функцией
или операторным коэффициентом
передачи рассматриваемой системы.
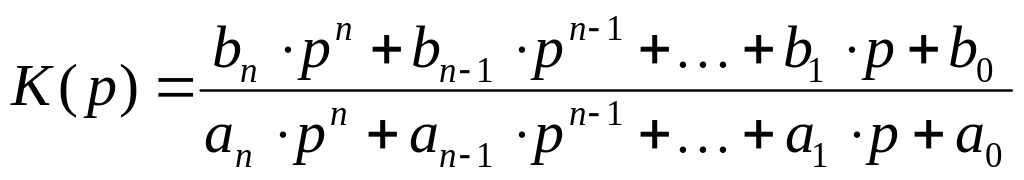 Если
эта функция известна, то поиск выходной
реакции системы на заданное входное
воздействие разбивается на три этапа:
Если
эта функция известна, то поиск выходной
реакции системы на заданное входное
воздействие разбивается на три этапа:
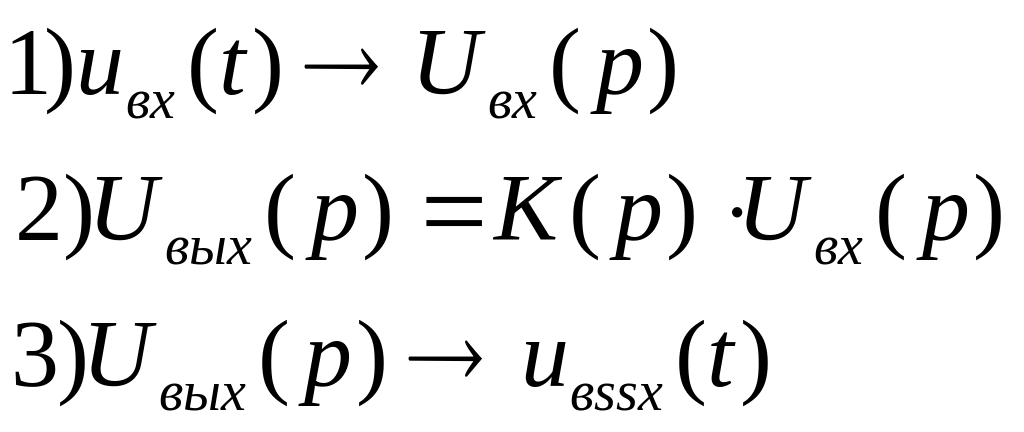
Функция
![]() есть
результат аналитического продолжения
частотного коэффициента передачи
есть
результат аналитического продолжения
частотного коэффициента передачи
![]() с
мнимой оси
с
мнимой оси
![]() на
всю плоскость комплексных частот
на
всю плоскость комплексных частот
![]() .
Функция
аналитична
на всей плоскости p,
за исключением конечного числа точек
.
Функция
аналитична
на всей плоскости p,
за исключением конечного числа точек
![]() ,
являющихся корнями знаменателя в формуле
К(р). Данные точки называют полюсами
передаточной функции К(р).
,
являющихся корнями знаменателя в формуле
К(р). Данные точки называют полюсами
передаточной функции К(р).
При практическом использовании операторного метода большую часть формальных вычислений можно исключить, обращаясь к широко распространенным таблицам преобразования Лапласа.
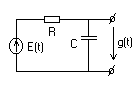
Анализ интегрирующей RC-цепи операторным методом при воздействии скачка.
Интегрирующая
RC-цепи показана на рисунке.
Здесь
![]()
 ,
поэтому
,
поэтому
![]() .
Разлагая эту функцию на эдементарные
дроби, имеем
.
Разлагая эту функцию на эдементарные
дроби, имеем
![]() .
Оригиналы соответствующие обоим
слагаемым в правой части формулы хорошо
известны. Искомый результат имеет вид
.
Оригиналы соответствующие обоим
слагаемым в правой части формулы хорошо
известны. Искомый результат имеет вид
![]()
Анализ интегрирующей RC-цепи операторным методом при воздействии прямоугольного импульса.
Пусть задана
длительность T и амплитуда
U0. Тогда входной
сигнал имеет изображение
![]() .
Множитель exp(-pT)
свидетельствует о сдвиге во времени на
величину T. Поэтому,
используя результат предыдущей задачи
можно записать
.
Множитель exp(-pT)
свидетельствует о сдвиге во времени на
величину T. Поэтому,
используя результат предыдущей задачи
можно записать
![]() .
Для наглядности последнюю формулу
целесообразно представить так:
.
Для наглядности последнюю формулу
целесообразно представить так:
![]()
22. Разновидности частотно-избирательных цепей и их частотные характеристики: последовательный и параллельный связный контуры.
Частотно-избирательные цепи пропускают на вход лишь колебания с частотами, которые лежат в относительно узкой полосе вокруг некоторой центральной частоты. Частотная фильтрация полезного сигнала особенно эффективна в том случае, если обрабатываемый сигнал в достаточной степени узкополосен.
П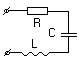 оследовательный
колебательный контур. Для
него частотные свойства могут быть
описаны его входной проводимостью
оследовательный
колебательный контур. Для
него частотные свойства могут быть
описаны его входной проводимостью
![]() .
На резонансной частоте
.
На резонансной частоте
![]() проводимость
контура чисто активная и равна
проводимость
контура чисто активная и равна
![]() .
Величину
.
Величину
![]() называют
характеристическим сопротивлением
контура. Частотно избирательные свойства
и полоса пропускания контура зависят
от ее добротности
называют
характеристическим сопротивлением
контура. Частотно избирательные свойства
и полоса пропускания контура зависят
от ее добротности
![]() .
Входное реактивное сопротивление вблизи
резонансной частоты будет
.
Входное реактивное сопротивление вблизи
резонансной частоты будет
![]() Полное входное сопротивление контура
Полное входное сопротивление контура
![]() ,
где
,
где
![]() .
Величины
.
Величины
![]() и
и
![]() называют,
соответственно, абсолютной и обобщенной
расстройкой. Амплитудно-частотной
характеристикой (АЧХ) контура называют
величину
называют,
соответственно, абсолютной и обобщенной
расстройкой. Амплитудно-частотной
характеристикой (АЧХ) контура называют
величину
![]() .
Величину
.
Величину
![]() называют
фазочастотной характеристикой контура.
Полоса пропускания контура находится
из соотношений:
называют
фазочастотной характеристикой контура.
Полоса пропускания контура находится
из соотношений:
![]() ,
где
,
где
![]() -
нормированное значение проводимости.
На границах полосы мощность сигнала в
контуре уменьшается вдвое.
-
нормированное значение проводимости.
На границах полосы мощность сигнала в
контуре уменьшается вдвое.
Параллельный и связный контуры. Для этих контуров известны следующие соотношения:
а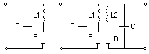 )
для параллельного контура
)
для параллельного контура
![]()
б) для связных
контуров
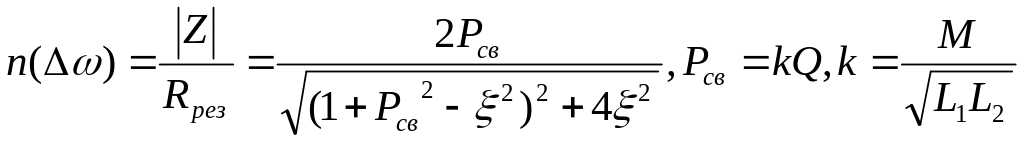 ,
,
где
![]() -
параметр связи, k –
коэффициент связи.
-
параметр связи, k –
коэффициент связи.
