19. Функция автокорреляции сигнала.
П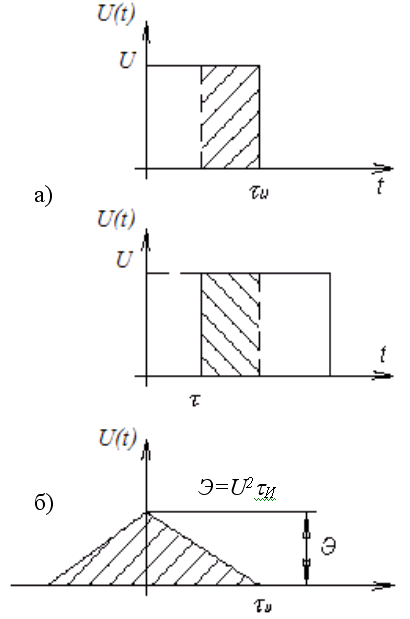
ри
обработке сигналов, например в РЛ
принятый отличается от излученного
прежде всего временем, положением,
которое и рассматривается как основной
измеряемый параметр. Математически
такие сигналы различают значениями
аргумента. Т. е. имеем два сигнала U(t)
и его сдвинутую копию U(t-).
Основным математическим понятием,
используемым при обработке сигналов,
является понятие функции автокорреляции.
Формируемой из сигналов и его сдвинутой
копии как величина их скалярного
произведения:
(10.1)
Взаимная энергия
переданного и принятого сигнала.
Очевидно, что при =0
получим
- это значение функции автокорреляции
является максимальным, т. е. при любых
0
(10.2)
Этот факт может
быть доказан с помощью неравенства
Шварца (4.15) (неравенство Коши - Буняковского)
имеющее следующий вид:
(4.15
а)
Функция автокорреляции
является четной функцией, что может
быть доказано подстановкой
;
и интегрированием получим:
(10.3)
Из этого равенства
и следует:
.
Т. о. функция автокорреляции представляет собой симметричную относительно оси ординат кривую с центральным и всегда положительным max и убывающая монотонно или с колебаниями с ростом временного сдвига .
Примеры определения функции автокорреляции.
а) Функция автокорреляции прямоугольного видеоимпульса.
Из графического
представления видно, что произведение
отличается от нуля только в приделах
заштрихованного участка наложения двух
сигналов. Если сдвиг не происходит
длительности импульсов, то этот временной
интервал (перекрытия) равен -И
и для последующего сигнала можно найти:
(10.4)
И корреляционная функция равна 0 если //>И. График этой функции представляет собой треугольник показанный на рис. 1 б.
б) Функция автокорреляции прямоугольного радиоимпульса.
.
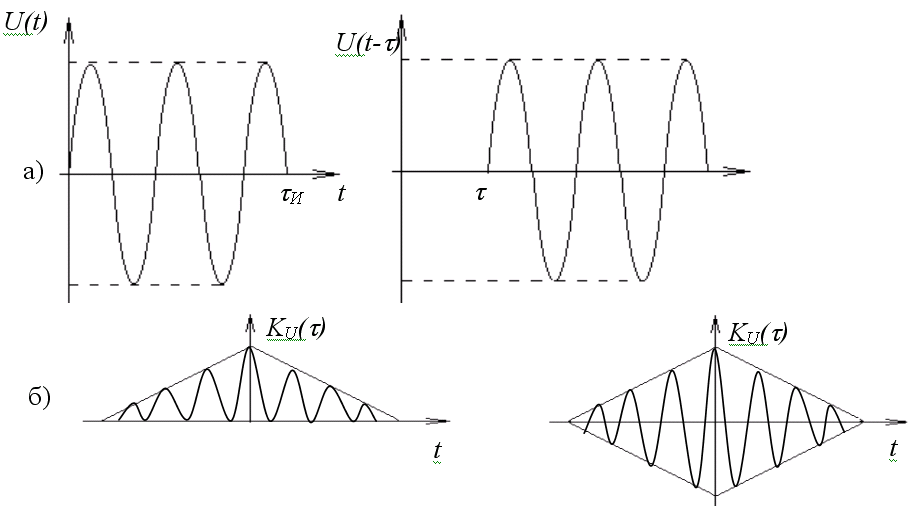
Значения функции автокорреляции можно
найти, используя известное тригонометрическое
соотношение вида:
Получим:
Считая, что на
границах интервала cos(И)
равен 0 и с учетом четности корреляционной
функции получим:
.
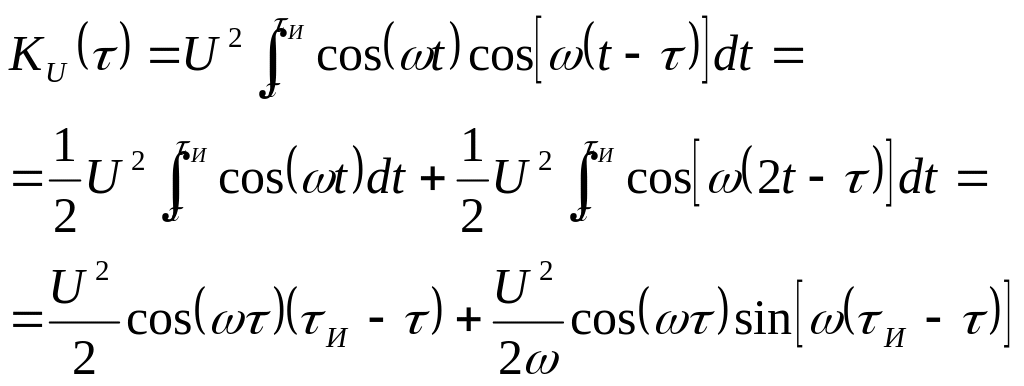
Графикэтойфункциинарис. б.
20. Функция автокорреляции неограниченно протяженного гармонического сигнала.
Рассмотренные выше выражения для АКФ может использоваться для сигналов имеющих ограниченную энергию. Если же сигнал не ограничен по энергии, но ограничен по мощности, то используют другую формулу представления АКФ.
Имеет смысл и размерности средней мощности во избежании расходимости интеграла новую функцию АК как физическое значение скалярного произведения сигнала и его копии.
Запись АКФ:
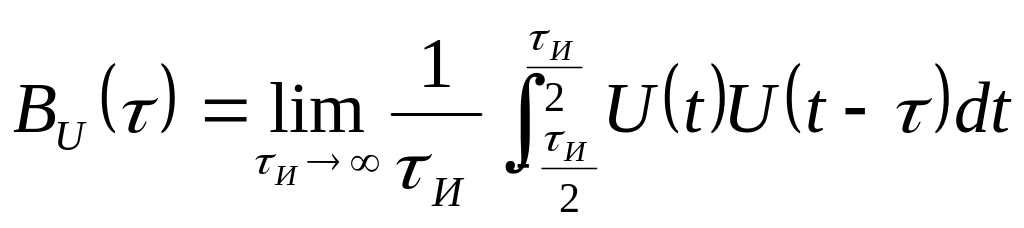(10.7)
Эта форма представления АКФ используется чаще, причем для периодической функции усреднения можно в приделах периода.
В качестве примера
найдем выражение для АКФ сигнала
.
Получим:
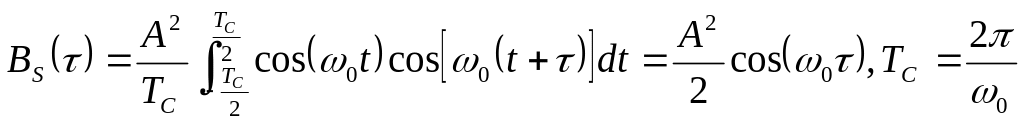(10.8)
При =0 BU(0)=A2/2. Это и есть средняя мощность колебания.