18. Взаимная спектральная плотность сигналов. Энергетический спектр.

Допустим, для обоих сигналов известны их спектры, тогда можно записать:

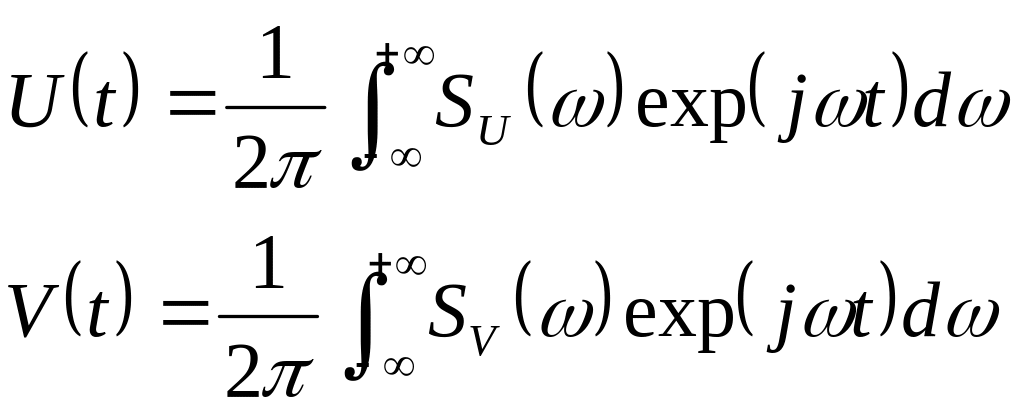(9.1)

здесь S_U() и S_V() спектральные плотности сигналов U(t) и V(t), подставим значение сигнала V(t) найденное по формуле (9.1) в скалярное произведение: . Изменим порядок интегрирования , где - спектр комплексно сопряженный. Учитывая, что изменение знака перед мнимой составляющей комплексного числа приводит к получению комплексно-сопряженной величины, а также, то обстоятельство, что скалярное произведение вещественных сигналов должно дать вещественный результат. приходим к выводу, что скалярное произведение может рассматриваться двух комплексно-сопряженных чисел: (9.2)

Полученное соотношение называют формулой Релея и читают так: cкалярное произведение двух сигналов пропорционально произведению спектральных плотностей.

Произведение (U,V) вещественно хотя и образовано произведением комплексных величин S_V() и S_U^*(). Из этого обстоятельства следует, что в подынтегральной функции может использоваться только реальная часть: (9.3)

И т. о. скалярное произведение (9.2) может быть переписано в виде: (9.10)

Функцию W_U,V() называют взаимным энергетическим спектром сигналов U(t) и V(t).

Примеры вычисления взаимных энергетических спектров некоторых сигналов.

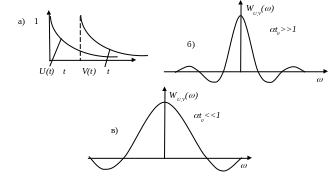
Рис. 9.1

Аналитически импульсы показанные на рис. 9.1, а и их спектры могут быть записаны в виде:

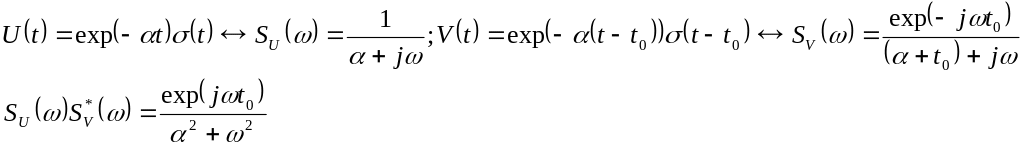
Энергетический спектр сигнала 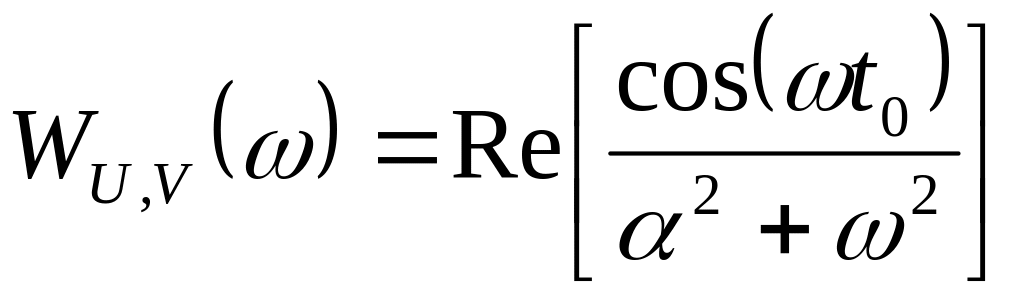(9.11)

Графики, показанные на рис. 9.1 б и в построены для разных значений константы t₀. При t₀<<1 график более растянут по отношению к t₀>>1.

В случае если : (9.12)

Полученные выражения для W_U,V() называется спектральной плотностью энергии сигнала и записывается так: (9.13)

Запись (9.13) представляет собой частный случай обобщенной формулы Релея и утверждает: энергия любого сигнала образуется и может быть вычислена как энергия всех частотных составляющих спектра сигнала. Эта формулировка аналогична рассмотренному ранее равенству Парсеваля, поэтому ее иногда называют равенством Парсеваля.

Анализ сигнала основанный на спектральных представлениях достаточно прост и удобен и отличается от метода преобразования Фурье тем, что в этом случае теряется информация о фазах спектральных составляющих сигналов. При таком подходе все сигналы одинаковые по форме, но различающиеся временным положением будут восприниматься оконечными устройствами как одинаковые сигналы т. е. не различимые, а это неверно. Однако этот подход очень полезен в тех случаях, когда фазы сигналов неопределенны например, в случае недетерминированных сигналов.

Задача определения энергетического спектра прямоугольного импульса.

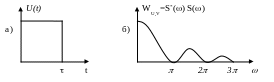
Рис. 9.2

, тогда

Из рис. 9.2 следует, что основная энергия сигнала сосредоточена в пределах первого низкочастотного лепестка. С ростом частоты средний вклад в энергию импульса высокочастотных компонент убывает обратно пропорционально квадрату частоты. Можно убедиться, что из формулы (9.13)

вычисление этого интеграла дает значение энергии

(9.14)

При анализе вопросов прохождения такого сигнала через физическую систему с ограниченной полосой пропускания (полоса ограничена первым лепестком). Численными методами вычисления интегралов можно найти: .

Такой подход не позволяет оценить степень искажения сигнала фильтром.