1. Понятие сигнала.
Сигналом (от лат. signum - знак) называется физический процесс или явление, несущее сообщение о каком-либо событии, состоянии объекта, либо передающее команды управления, оповещения и т.д. Таким образом, сигнал является материальным носителем сообщения. Таким носителем может служить любой физический процесс (свет, электрическое поле, звуковые колебания и т.п.). В радиоэлектронике изучаются и используются в основном электрические сигналы. Сигналы как физические процессы наблюдаются с помощью различных приборов и устройств (осциллографом, вольтметров, приемников). Любая модель отражает ограниченное число наиболее существенных признаков реального физического сигнала. Несущественные признаки сигнала игнорируются для упрощения математического описания сигналов. Общим требованием к математической модели является максимальное приближение к реальному процессу при минимальной сложности модели. Функции, описывающие сигналы могут принимать вещественные и комплексные значения, поэтому часто говорят о вещественных и комплексных моделях сигналов.
Классификация сигналов. По возм-ти предсказания мгн. значений сигнала в любой момент времени разл-ют:
- Детерминированные сигналы, т.е. такие сигналы, для которых мгновенные значения для любого момента времени известны и предсказуемы с вероятностью равной единице;
- Случайные сигналы, т.е. такие сигналы, значение которых в любой момент времени невозможно предсказать с вероятностью равной единице.
Все сигналы, несущие информацию являются случайными, поскольку полностью детерминированный сигнал (известный) информации не содержит.
Простейшими примерами детерминированного и случайного сигналов являются напряжения сети и напряжения шума соответственно (см. рис.2.1).
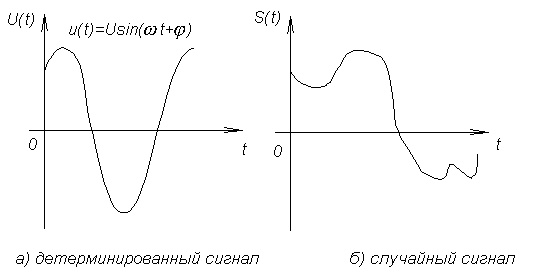
В свою очередь случайные и детерминированные сигналы могут подразделяться на непрерывные или аналоговые сигналы и дискретные сигналы, имеющие несколько разновидностей. Если сигнал можно измерять (наблюдать) в любой момент времени, то его называют аналоговым. Такой сигнал существует в любой момент времени. Дискретные сигналы могут наблюдаться и измеряться в дискретные (отдельные) ограниченные по длительности к моменту появления отрезки времени. К дискретным сигналам относятся импульсные сигналы.
Н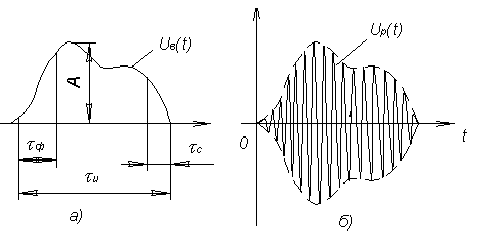
а
рисунке показаны два вида импульсов.
Видеоимпульс
и радиоимпульс
.
При формировании радиоимпульсов
видеоимпульс используется как управляющий
(модулирующий) сигнал и в этом случае
между ними существует аналитическая
связь:
. (2.1)
При этом
называется огибающей радиоимпульса, а
функция
- его заполнением.
И
мпульсы
принято характеризовать амплитудой A,
длительностью
,
длительностью фронта
и среза
и при необходимости частотой
или периодом
повторения.
Импульсные сигналы могут быть самых различных видов. В частности различают импульсные сигналы называемые дискретными (см. рис.2.3).
Эта разновидность
сигналов может быть представлена
математической моделью в виде счетного
множества значений функции
- где i = 1, 2, 3, ...., k, отсчитываемых в
дискретные моменты времени
.
Шаг дискретизации сигнала по времени
и по амплитуде обычно величина постоянная
для данного типа сигнала, т.е. минимальное
приращение сигнала
;
Каждое из значений
конечного множества S можно представить
в двоичной системе исчисления в виде
числа:
- 10101;
- 11001;
- 10111. Такие сигналы называют цифровыми.