Лекция . Фактор времени. Дисконт. Норма дисконта.

1. Стоимость денег во времени. Дисконтирование

В наиболее общем виде смысл понятия «стоимость денег во времени» может быть выражен фразой  рубль, имеющийся в распоряжении сегодня, и рубль, ожидаемый к получению в некотором будущем, не равны, а именно: первый имеет большую ценность по сравнению со вторым по двум причинам.

Первой причиной является обесценивание денег с течением времени из-за инфляции.

Вторая причина связана с обращением денежных средств. Рубль, вложенный в любого рода коммерческие операции (включая и простое помещение его на депозит в банке), способен через некоторое время превратиться в большую сумму за счет полученного с его помощью дохода.

Эта истина является аксиомой финансовых операций и предопределяет весь механизм экономического обоснования и анализа инвестиционных проектов.

Наиболее простым и очевидным примером справедливости этой аксиомы является динамика средств, внесенных на сберегательный счет в банке.

Предположим, что мы сегодня можем положить 1000 руб. на депозит под 5 % годовых. Через год сумма на сберегательном счете составит 1050 руб.

В нашем примере будущая стоимость (future value или FV) сегодняшних 1000 руб. при ставке 5 % годовых составит 1050 руб.

,

,

Если мы не будем изымать деньги из банка и оставим их там на второй и третий годы, то окончательная сумма после завершения двухлетнего и трехлетнего периода соответственно составит:

;

Эта модель умножения сбережений, известная как модель сложных процентов, в общем виде может быть записана следующим образом:

, (1)

Где:

FV – будущая величина той суммы, которую мы инвестируем в любой форме сегодня и которой будем располагать через интересующий нас период времени, в течение которого эти деньги будут работать;

PV (present value) – текущая (современная) величина той суммы, которую мы инвестируем ради получения дохода в будущем;

E – величина доходности инвестиций, в данном примере она равна ставке банковского процента по сберегательному вкладу, а в более общем случае – прибыльности инвестиций;

к – число стандартных периодов времени, в течение которых наши инвестиции будут участвовать в коммерческом обороте.

Если проценты не причисляются к вкладу, а начисляются только за определенный период, то мы имеем дело с простыми процентами.

Расчет будущей величины вложенной суммы в этом случае определяется по формуле:

FV = PV (1 + k· E)

Начисление простых процентов используют при краткосрочных кредитах.

Решим обратную задачу, т.е. определить текущую (современную) стоимость (PV) (или определение того, сколько надо было бы инвестировать сегодня, чтобы получить некоторую сумму в будущем).

Для осуществления такого расчета используется формула, которая является обратной по смыслу формуле (1):

PV= . (2)

Следовательно, текущая (современная) стоимость равна будущей стоимости, умноженной на коэффициент , называемый коэффициентом дисконтирования.

В нашем примере текущая стоимость (PV) 1000 руб., которые будут получены через 3 года при 5 % годовых, составит:

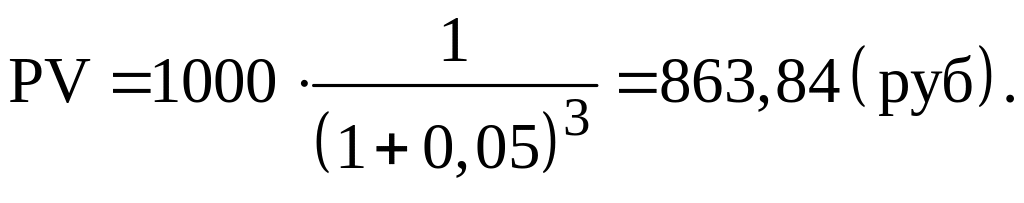
Определяя величину текущей стоимости (PV) исходя из суммы будущей стоимости, мы проводим дисконтирование будущей стоимости.

Дисконтированием называется процесс приведения (корректировки) будущей стоимости денег к их текущей (современной стоимости). Процесс, обратный дисконтированию, а именно, определение будущей стоимости, есть не что иное, как начисление сложных процентов на первоначально инвестируемую стоимость.

Процессы начисления сложных процентов и дисконтирования являются столь же древними, как и сам процесс кредитования, и используются финансовыми институтами с незапамятных времен.