6. Модель параллелизма данных

Название модели происходит оттого, что она эксплуатирует параллелизм, который заключается в применении одной и той же операции к множеству элементов структур данных.

• Используется естественный параллелизм приложения или некой однотипной операции над элементами структуры данных например, «добавляется 2 к всем элементам этой таблицы» или «увеличивается оклад всех служащих со стажем свыше 5 лет»

• Программа с параллелизмом данных состоит из последовательности таких операций

• Компиляторы, использующие параллелизм данных, часто требуют, чтобы программист явно указал распределение данных по процессорам.

7. Модель разделяемой памяти

• Задачи разделяют общее адресное пространство, чтение и запись в него выполняется асинхронно.

• Для управления доступом к общей памяти могут использоваться различные механизмы типа блокировок и семафоров.

• Преимущество этой модели с точки зрения программиста – отсутствует понятие «собственника» данных, и, следовательно, нет необходимости явно указывать способ передачи данных от производителей потребителям. Это упрощает разработку программы.

• Понимание и управление локализацией данных более сложное.

• Разработка детерминированных программ затруднена.

8. Понятие о детерминизме программы

Детерминизм – предсказуемое поведение программы в процессе ее исполнения.

Параллельная программа может давать разные результаты при повторных запусках даже без модификации кода и исходных данных. Это является следствием «гонок за данными» - одновременного и асинхронного доступа разных процессов или потоков к общим переменным

Хотя недетерминизм иногда является полезным и его стараются поддерживать, для параллельного программирования желательно выполнение условия детерминизма программы. Детерминированные программы просты для понимания. Например, отследить корректность программы проще по результату одного исполнения, чем по множеству всех возможных

9. Модульность. Виды композиции модулей и/или программ

Модульность (modularity) – возможность декомпозиции сложных программ на простые компоненты:

• Процедуры

• Структуры данных

• ОО-конструкции

• т.п.

Программы часто создаются как набор отдельных частей, взаимодействующих друг с другом для получения нужного результата. Программа может представлять собой единую сложную структуру, выполняющую несколько функций с помощью различных частей программы. Однако более простым решением является создание нескольких модулей, которые совместно используют системные ресурсы, но выполняют каждый свою функцию.

В программе, состоящей из нескольких модулей, каждый модуль имеет собственное назначение и выполняет отдельный набор действий. Эти модули независимы друг от друга, они взаимодействуют только при передаче информации. При этом для обеспечения целостности данных необходимо синхронизировать работу модулей.

10. Пример параллельного алгоритма: конечные разности.

Параллельный алгоритм для конечно-разностной задачи. Дан вектор X где N=8. Весь пример разделён на 8 подзадач (далее просто задачи), каждая из которых инкапсулирует только свои данные и взаимодействует с соседями слева и справа через каналы. В структуре каждой задачи есть два входных и выходных порта. (Термин «задача» - обобщающий и используется потому, что это может быть как отдельный узел (процессор), так и просто поток в рамках одного узла).

Дано 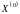на каждой задаче. Найти на каждой задаче.

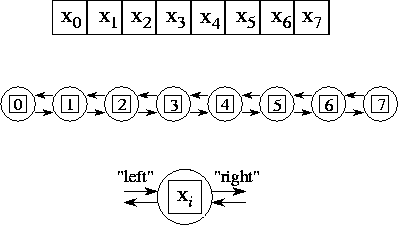
Параллельный алгоритм для данного примера подразумевает создание N задач, по одной на каждую точку в векторе . Начальное условие 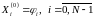примера разделено между всеми задачами: в i-ой задаче дано и она отвечает за вычисление значений в течение всех шагов T. Поэтому на каждом шаге t для вычисления очередного значения данная задача должна получить числа 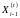и от своих соседей слева (i-1) и справа (i+1) соответственно, как показано на рисунке выше. Для этого каждая задача (кроме 0-ой и (N-1)-ой, потому что для них новые значения по времени вычисляются из граничных условий – курс ЧМ©) делает следующие действия:

1. Посылает своё текущее значение соседу слева и справа;

2. Получает значения и от левого и правого соседа;

3. Использует полученные значения для вычисления 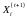по формуле выше.