1. Линейная алгебра

1.1. Матрицы

Матрица – это совокупность чисел, расположенных в виде прямоугольной таблицы. Складывать матрицы можно только одинаковых размеров. При этом получается матрица тех же размеров, элементы которой равны сумме элементов матриц-слагаемых, стоящих на одинаковых местах. При умножении матрицы на число, каждый ее элемент умножается на это число.

Произведением матриц А и В называется матрица С, любой элемент c_ij которой состоит из суммы парных произведений элементов i-й строки первой матрицы на элементы j-го столбца второй матрицы. Говорят, что при перемножении матриц действует правило: «строка умножается на столбец». Заметим, что не всякие матрицы можно перемножать.

Пример 1.1. Перемножить матрицы:

а)

б)

Пример 1.2. Перемножить матрицы:

.

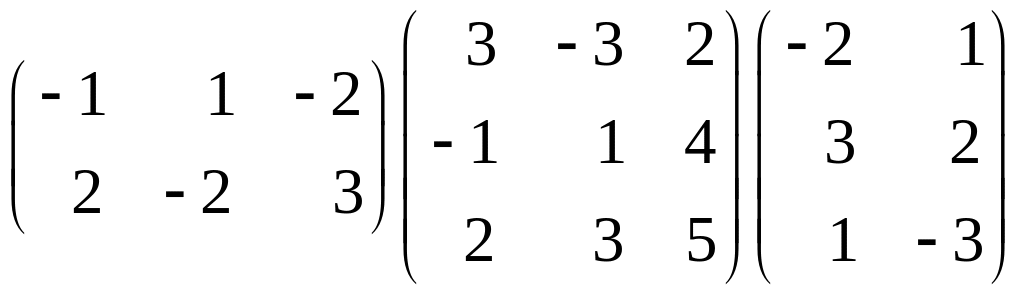Решение. Для операции умножения матриц справедлив ассоциативный закон умножения: A(BC)=(AB)C. Поэтому данное задание выполним двумя способами.

Способ 1. Перемножим первые две матрицы:

.

Затем результат умножим на третью матрицу:

.

Способ 2. Перемножим последние две матрицы:

.

Затем результат умножим на первую матрицу:

.

Как и следовало ожидать, результат получился тот же самый.

1.2. Определители

Определитель есть число, полученное из элементов матрицы A и характеризующее её. Матрицы обычно обозначаются символами: det A, |A| или ..

О

(1.1)

пределитель второго порядка находится следующим образом:

Он равен произведению элементов главной диагонали матрицы минус произведение элементов второй диагонали. Например:

Определитель матрицы 3-го порядка находится следующим образом

(1.2)

Естественно, что запомнить эту формулу довольно трудно. Однако есть правила, которые облегчают выписывание выражения для определителя 3-го порядка. Например,

П равило треугольников: три слагаемых, входящих в исходное выражение со знаком плюс, есть произведения элементов главной диагонали или треугольников, основания которых параллельны этой диагонали. Остальные три слагаемых, входящие со знаком минус, находятся таким же образом, но относительно второй диагонали.

Пример 1.3. Вычислить определитель

Дополнительным минором M_ij элемента a_ij называется определитель, получаемый из данного путем вычеркивания i-й строки и j-го столбца. Алгебраическим дополнением A_ij элемента a_ij называется минор этого элемента, взятого со знаком (–1)^i+j, т.е. A_ij = (–1)^i+jM_ij.

Используя понятие алгебраического дополнения можно сформулировать теорему о разложении определителя n-го порядка по строке или столбцу.

Теорема. Определитель матрицы A равен сумме произведений всех элементов некоторой строки (или столбца) на их алгебраические дополнения:

Данная теорема лежит в основе одного из основных методов вычисления определителей, т.н. метода понижения порядка.

Свойство 1. Определитель не изменится, если в нем поменять местами строки и столбцы, т.е. при транспонировании матрицы:

.

Данное свойство свидетельствует о равноправии строк и столбцов определителя. Иначе говоря, любое утверждение о столбцах определителя справедливо и для его строк и наоборот.

Свойство 2. Определитель меняет знак при перестановке двух строк (столбцов).

Свойство 3. Если определитель имеет две одинаковые строки (столбца), то он равен нулю.

Свойство 4. Общий множитель всех элементов какой-либо строки (столбца) можно вынести за знак определителя.

Например:

Свойство 5. Если все элементы некоторой строки (столбца) определителя равны нулю, то и сам определитель равен нулю.

Свойство 6. Определитель не изменится, если к элементам одной строки (столбца), прибавить элементы другой строки (столбца), умноженной на какое-либо число.

Свойство 7. Определитель треугольной матрицы равен произведению элементов, стоящих на главной диагонали:

.

Пример 1.4. Вычислить определитель:

.

Решение. Упростим данный определитель, а затем вычислим его, разложив его по элементам 2-й строки:

.

Пример 1.5. Вычислить определитель:

.

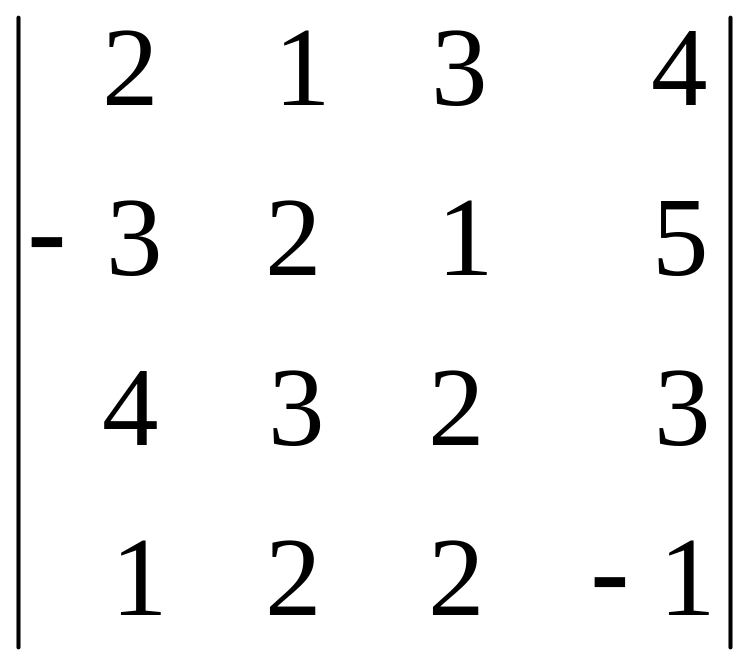Решение. Способ 1.При помощи элементарных преобразований матрицы, учитывая свойства определителей, будем получать в какой-либо строке или столбце нули, а затем будем разлагать полученный определитель по этой строке или столбцу:

.

С пособ 2.При помощи элементарных преобразований матрицы, учитывая свойства определителей, приведем матрицу к треугольному виду:

.